Question Number 117754 by bemath last updated on 13/Oct/20
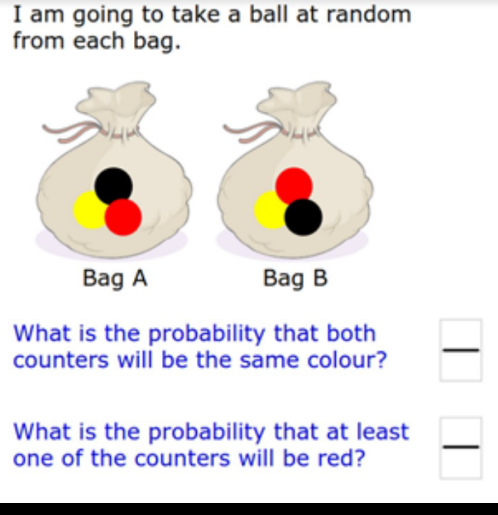
Commented by bemath last updated on 13/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
Answered by bobhans last updated on 13/Oct/20
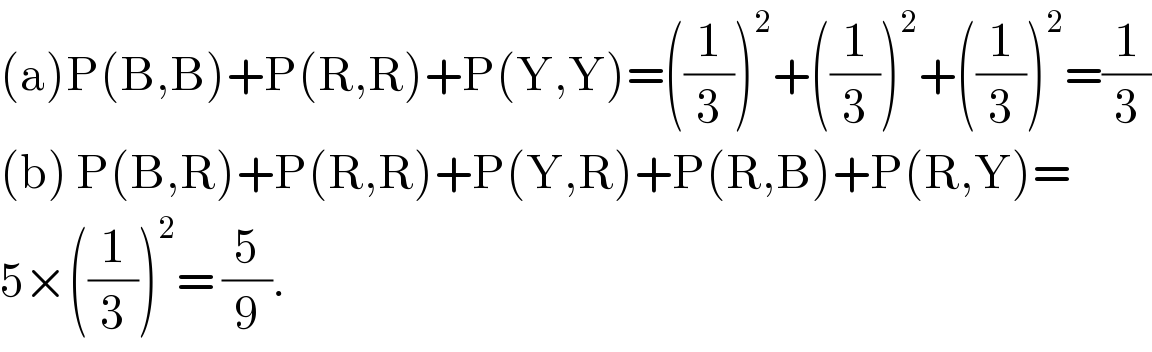
$$\left(\mathrm{a}\right)\mathrm{P}\left(\mathrm{B},\mathrm{B}\right)+\mathrm{P}\left(\mathrm{R},\mathrm{R}\right)+\mathrm{P}\left(\mathrm{Y},\mathrm{Y}\right)=\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{P}\left(\mathrm{B},\mathrm{R}\right)+\mathrm{P}\left(\mathrm{R},\mathrm{R}\right)+\mathrm{P}\left(\mathrm{Y},\mathrm{R}\right)+\mathrm{P}\left(\mathrm{R},\mathrm{B}\right)+\mathrm{P}\left(\mathrm{R},\mathrm{Y}\right)= \\ $$$$\mathrm{5}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} =\:\frac{\mathrm{5}}{\mathrm{9}}. \\ $$
Answered by MJS_new last updated on 13/Oct/20
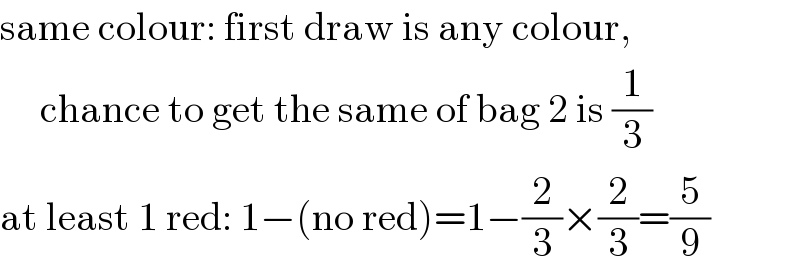
$$\mathrm{same}\:\mathrm{colour}:\:\mathrm{first}\:\mathrm{draw}\:\mathrm{is}\:\mathrm{any}\:\mathrm{colour}, \\ $$$$\:\:\:\:\:\mathrm{chance}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{of}\:\mathrm{bag}\:\mathrm{2}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{at}\:\mathrm{least}\:\mathrm{1}\:\mathrm{red}:\:\mathrm{1}−\left(\mathrm{no}\:\mathrm{red}\right)=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{9}} \\ $$
