Question Number 117787 by mathdave last updated on 13/Oct/20
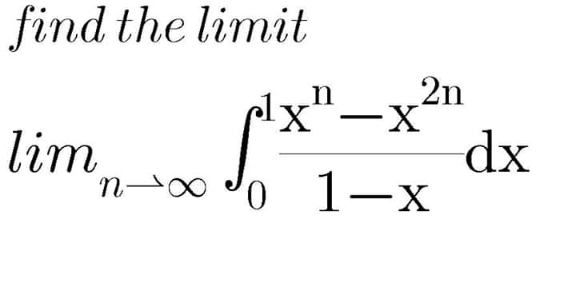
Answered by Dwaipayan Shikari last updated on 13/Oct/20
![lim_(n→∞) ∫_0 ^1 x^n ((1−x^n )/(1−x))dx =lim_(n→∞) ∫_0 ^1 x^n (1+x+x^2 +...x^(n−1) )dx =lim_(n→∞) (1/(n+1))+(1/(n+2))+....+(1/(2n)) =(1/n)lim_(n→∞) Σ_(k=1) ^n (1/(1+(k/n))) =∫_0 ^1 (1/(1+x))dx=[log(1+x)]_0 ^1 =log(2)](https://www.tinkutara.com/question/Q117797.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \frac{\mathrm{1}−{x}^{{n}} }{\mathrm{1}−{x}}{dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…{x}^{{n}−\mathrm{1}} \right){dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}+….+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$=\frac{\mathrm{1}}{{n}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\left[{log}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} ={log}\left(\mathrm{2}\right) \\ $$
Answered by mathmax by abdo last updated on 13/Oct/20
![A_n =∫_0 ^1 ((x^n −x^(2n) )/(1−x))dx ⇒A_n =∫_0 ^1 ((x^n (1−x^n ))/(1−x))dx =∫_0 ^1 ((x^n (1−x)(1+x+x^2 +...+x^(n−1) ))/(1−x))dx =∫_0 ^1 (x^n +x^(n+1) +x^(n+2) +...+x^(2n−1) )dx =[(x^(n+1) /(n+1)) +(x^(n+2) /(n+2))+....+(x^(2n) /(2n))]_0 ^1 =(1/(n+1))+(1/(n+2))+....+(1/(n+n)) =Σ_(k=1) ^n (1/(n+k)) ⇒lim_(n→+∞) A_n =lim_(n→+∞) (1/n)Σ^n _(k=1) (1/(1+(k/n))) =∫_0 ^1 (dx/(1+x)) =[ln(1+x)]_0 ^1 =ln(2)](https://www.tinkutara.com/question/Q117840.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{n}} \right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} +…+\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} +\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{x}^{\mathrm{n}+\mathrm{2}} \:+…+\mathrm{x}^{\mathrm{2n}−\mathrm{1}} \right)\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\frac{\mathrm{x}^{\mathrm{n}+\mathrm{2}} }{\mathrm{n}+\mathrm{2}}+….+\frac{\mathrm{x}^{\mathrm{2n}} }{\mathrm{2n}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}+….+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{n}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\sum}^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}}\:=\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{ln}\left(\mathrm{2}\right) \\ $$
