Question Number 117912 by A8;15: last updated on 14/Oct/20

Commented by A8;15: last updated on 14/Oct/20
help please
Answered by Lordose last updated on 14/Oct/20
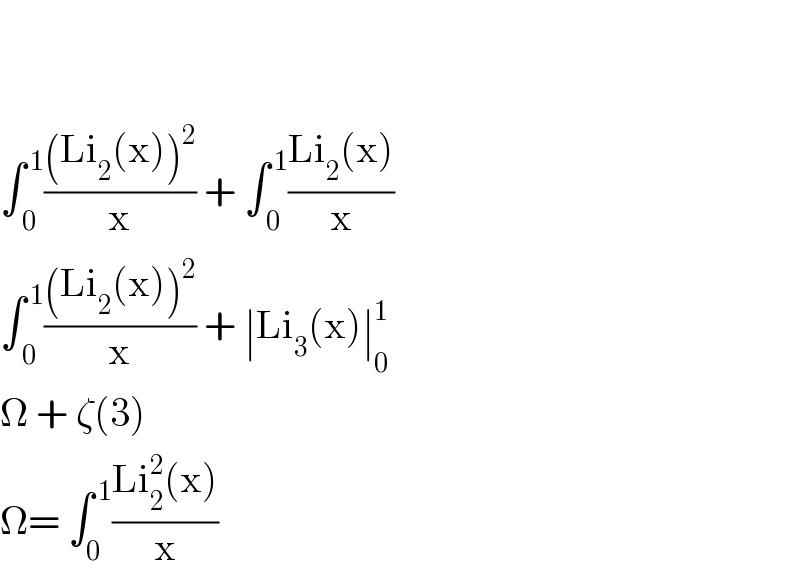
$$ \\ $$$$ \\ $$$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} }{\mathrm{x}}\:+\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}} \\ $$$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} }{\mathrm{x}}\:+\:\mid\mathrm{Li}_{\mathrm{3}} \left(\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:+\:\zeta\left(\mathrm{3}\right) \\ $$$$\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}} \\ $$
