Question Number 117960 by andilizhaa last updated on 14/Oct/20

Answered by mathmax by abdo last updated on 14/Oct/20
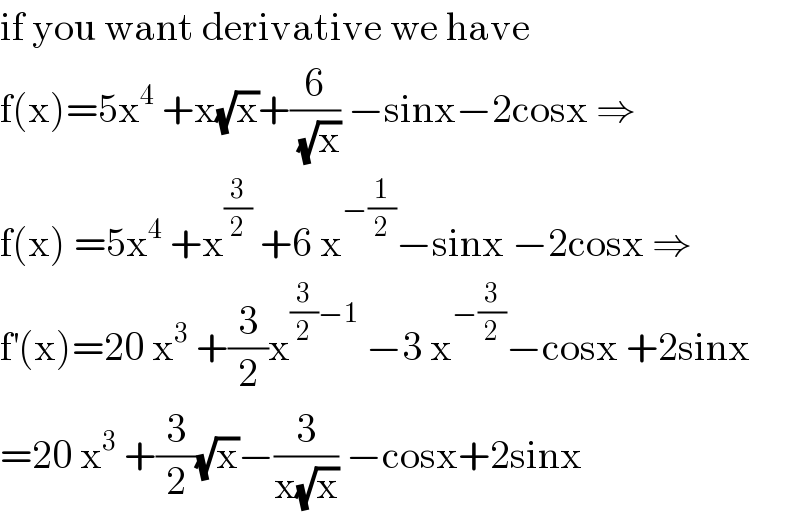
$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{derivative}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{5x}^{\mathrm{4}} \:+\mathrm{x}\sqrt{\mathrm{x}}+\frac{\mathrm{6}}{\:\sqrt{\mathrm{x}}}\:−\mathrm{sinx}−\mathrm{2cosx}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{5x}^{\mathrm{4}} \:+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\mathrm{6}\:\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{sinx}\:−\mathrm{2cosx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{20}\:\mathrm{x}^{\mathrm{3}} \:+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \:−\mathrm{3}\:\mathrm{x}^{−\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{cosx}\:+\mathrm{2sinx} \\ $$$$=\mathrm{20}\:\mathrm{x}^{\mathrm{3}} \:+\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{x}}−\frac{\mathrm{3}}{\mathrm{x}\sqrt{\mathrm{x}}}\:−\mathrm{cosx}+\mathrm{2sinx} \\ $$
