Menu Close

Question-118011

Tinku Tara 0 Comments
Pin




Question Number 118011 by mmmmmm1 last updated on 14/Oct/20
Answered by mr W last updated on 14/Oct/20
(x−h)^2 +(y−k)^2 =R^2 (0−h)^2 +(0−k)^2 =R^2 ...(i) (−4−h)^2 +(0−k)^2 =R^2 ...(ii) (2−h)^2 +(−3−k)^2 =R^2 ...(iii) (ii)−(i): 4(4+2h)=0 ⇒h=−2 (iii)−(i): 2(2−2h)+3(3+2k)=0 ⇒k=−(7/2) R^2 =(2)^2 +((7/2))^2 =((65)/4) ⇒R=((√(65))/2)
$$\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{0}−{h}\right)^{\mathrm{2}} +\left(\mathrm{0}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:…\left({i}\right) \\ $$$$\left(−\mathrm{4}−{h}\right)^{\mathrm{2}} +\left(\mathrm{0}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:…\left({ii}\right) \\ $$$$\left(\mathrm{2}−{h}\right)^{\mathrm{2}} +\left(−\mathrm{3}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:…\left({iii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\mathrm{4}\left(\mathrm{4}+\mathrm{2}{h}\right)=\mathrm{0}\:\Rightarrow{h}=−\mathrm{2} \\ $$$$\left({iii}\right)−\left({i}\right): \\ $$$$\mathrm{2}\left(\mathrm{2}−\mathrm{2}{h}\right)+\mathrm{3}\left(\mathrm{3}+\mathrm{2}{k}\right)=\mathrm{0}\:\Rightarrow{k}=−\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} =\left(\mathrm{2}\right)^{\mathrm{2}} +\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{65}}{\mathrm{4}} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 14/Oct/20
it′s the circumcircle of a triangle with a=4 b=(√(2^2 +3^2 ))=(√(13)) c=(√((2+4)^2 +3^2 ))=(√(45)) R=((abc)/( (√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))))=((√(65))/2) ⇒ area of circle=((65π)/4)
$$\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with} \\ $$$${a}=\mathrm{4} \\ $$$${b}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\mathrm{13}} \\ $$$${c}=\sqrt{\left(\mathrm{2}+\mathrm{4}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\mathrm{45}} \\ $$$${R}=\frac{{abc}}{\:\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{area}\:\mathrm{of}\:\mathrm{circle}=\frac{\mathrm{65}\pi}{\mathrm{4}} \\ $$
Answered by mr W last updated on 14/Oct/20
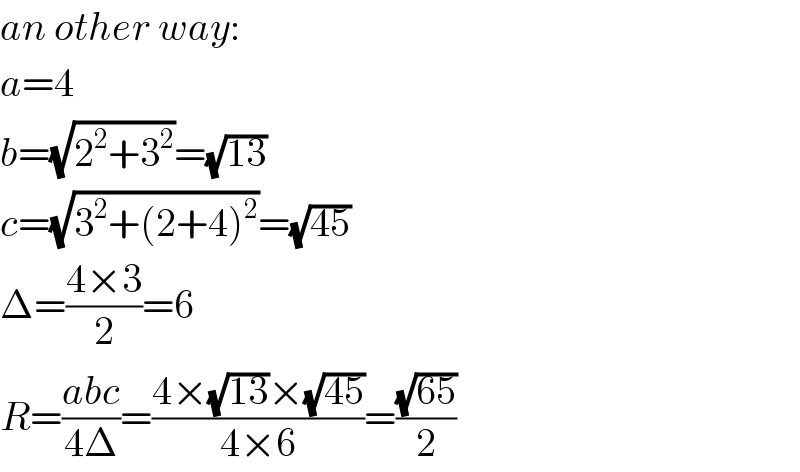
an other way: a=4 b=(√(2^2 +3^2 ))=(√(13)) c=(√(3^2 +(2+4)^2 ))=(√(45)) Δ=((4×3)/2)=6 R=((abc)/(4Δ))=((4×(√(13))×(√(45)))/(4×6))=((√(65))/2)
$${an}\:{other}\:{way}: \\ $$$${a}=\mathrm{4} \\ $$$${b}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\mathrm{13}} \\ $$$${c}=\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{4}\right)^{\mathrm{2}} }=\sqrt{\mathrm{45}} \\ $$$$\Delta=\frac{\mathrm{4}×\mathrm{3}}{\mathrm{2}}=\mathrm{6} \\ $$$${R}=\frac{{abc}}{\mathrm{4}\Delta}=\frac{\mathrm{4}×\sqrt{\mathrm{13}}×\sqrt{\mathrm{45}}}{\mathrm{4}×\mathrm{6}}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Answered by 1549442205PVT last updated on 15/Oct/20
Commented by 1549442205PVT last updated on 15/Oct/20
Given AC=4,CD=3,DB=2 ACD^(�) =CDB^(�) =90° first way: AC//BD⇒((DH)/(HC))=((BD)/(AC))=(2/4)=(1/2) CD=3(hypothesis)⇒HC=2 AH=(√(AC^2 +CH^2 ))=(√(4^2 +2^2 ))=2(√5) sinCAH^(�) =((CH)/(AH))=(2/(2(√5)))=(1/( (√5))) sinCLB^(�) =sinCAB^(�) =sinCAH^(�) =1/(√5) ΔBCL is right at B⇒2R=CL=((BC)/(sinCLB^(�) )) =((√(3^2 +2^2 ))/((1/(√5))))=(√(65))⇒R=(√(65))/2 ⇒S_(circle) =πR^2 =((65π)/4) second way:Suppose (CD)∩(O)=E Denote by I,F midpoint AC,CE respectively Put DF=x ⇒BF=x+3,J=(BD)∩OI ⇒BJ⊥OI(since OI⊥AC,AC//BJ) ⇒OJ=DF=x,CI=DJ=2,BJ=4 so in the righttriangles OFC and OJB we have:(x+3)^2 +2^2 =R^2 =x^2 +4^2 ⇒x^2 +6x+13=x^2 +16⇒6x=3⇒x=(1/2) ⇒R=(√(x^2 +4^2 ))=(√((1/4)+16))=(√((65)/4))=((√(65))/2) ⇒S_(circle) =((65π)/4)
$$\mathrm{Given}\:\mathrm{AC}=\mathrm{4},\mathrm{CD}=\mathrm{3},\mathrm{DB}=\mathrm{2} \\ $$$$\widehat {\mathrm{ACD}}=\widehat {\mathrm{CDB}}=\mathrm{90}° \\ $$$$\mathrm{first}\:\mathrm{way}: \\ $$$$\mathrm{AC}//\mathrm{BD}\Rightarrow\frac{\mathrm{DH}}{\mathrm{HC}}=\frac{\mathrm{BD}}{\mathrm{AC}}=\frac{\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{CD}=\mathrm{3}\left(\mathrm{hypothesis}\right)\Rightarrow\mathrm{HC}=\mathrm{2} \\ $$$$\mathrm{AH}=\sqrt{\mathrm{AC}^{\mathrm{2}} +\mathrm{CH}^{\mathrm{2}} }=\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{sin}\widehat {\mathrm{CAH}}=\frac{\mathrm{CH}}{\mathrm{AH}}=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{5}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{sin}\widehat {\mathrm{CLB}}=\mathrm{sin}\widehat {\mathrm{CAB}}=\mathrm{sin}\widehat {\mathrm{CAH}}=\mathrm{1}/\sqrt{\mathrm{5}} \\ $$$$\Delta\mathrm{BCL}\:\mathrm{is}\:\mathrm{right}\:\mathrm{at}\:\mathrm{B}\Rightarrow\mathrm{2R}=\mathrm{CL}=\frac{\mathrm{BC}}{\mathrm{sin}\widehat {\mathrm{CLB}}} \\ $$$$=\frac{\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}{\left(\mathrm{1}/\sqrt{\mathrm{5}}\right)}=\sqrt{\mathrm{65}}\Rightarrow\mathrm{R}=\sqrt{\mathrm{65}}/\mathrm{2} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{circle}} =\pi\mathrm{R}^{\mathrm{2}} =\frac{\mathrm{65}\pi}{\mathrm{4}} \\ $$$$\mathrm{second}\:\mathrm{way}:\mathrm{Suppose}\:\left(\mathrm{CD}\right)\cap\left(\mathrm{O}\right)=\mathrm{E} \\ $$$$\mathrm{Denote}\:\mathrm{by}\:\mathrm{I},\mathrm{F}\:\mathrm{midpoint}\:\mathrm{AC},\mathrm{CE}\:\mathrm{respectively} \\ $$$$\mathrm{Put}\:\mathrm{DF}=\mathrm{x}\:\Rightarrow\mathrm{BF}=\mathrm{x}+\mathrm{3},\mathrm{J}=\left(\mathrm{BD}\right)\cap\mathrm{OI} \\ $$$$\Rightarrow\mathrm{BJ}\bot\mathrm{OI}\left(\mathrm{since}\:\mathrm{OI}\bot\mathrm{AC},\mathrm{AC}//\mathrm{BJ}\right) \\ $$$$\Rightarrow\mathrm{OJ}=\mathrm{DF}=\mathrm{x},\mathrm{CI}=\mathrm{DJ}=\mathrm{2},\mathrm{BJ}=\mathrm{4} \\ $$$$\mathrm{so}\:\mathrm{in}\:\mathrm{the}\:\mathrm{righttriangles}\:\mathrm{OFC}\:\mathrm{and}\:\mathrm{OJB} \\ $$$$\mathrm{we}\:\mathrm{have}:\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{13}=\mathrm{x}^{\mathrm{2}} +\mathrm{16}\Rightarrow\mathrm{6x}=\mathrm{3}\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{R}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }=\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{16}}=\sqrt{\frac{\mathrm{65}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{circle}} =\frac{\mathrm{65}\pi}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *