Question Number 118203 by aurpeyz last updated on 15/Oct/20
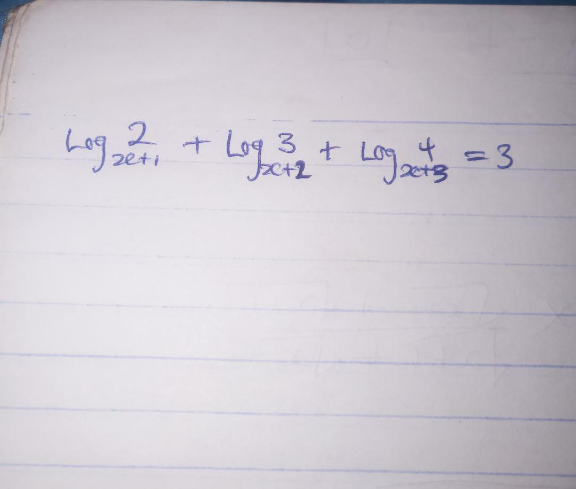
Answered by MJS_new last updated on 15/Oct/20

$$\mathrm{at}\:\mathrm{first}\:\mathrm{glance}\:{x}=\mathrm{1} \\ $$
Commented by aurpeyz last updated on 17/Oct/20

$${workings}? \\ $$
Commented by MJS_new last updated on 17/Oct/20
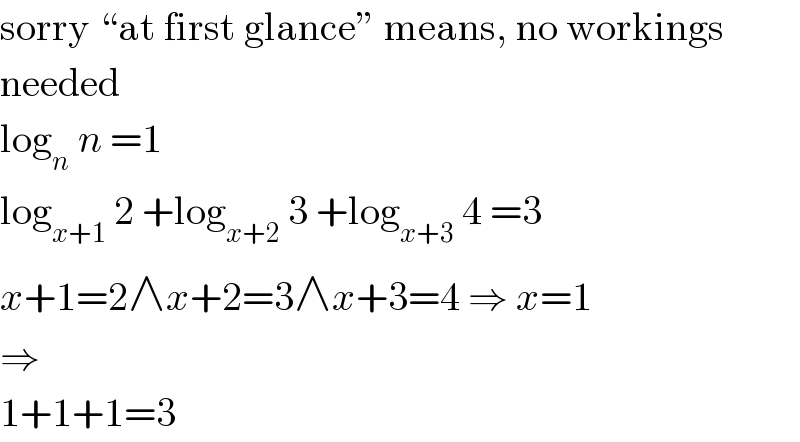
$$\mathrm{sorry}\:“\mathrm{at}\:\mathrm{first}\:\mathrm{glance}''\:\mathrm{means},\:\mathrm{no}\:\mathrm{workings} \\ $$$$\mathrm{needed} \\ $$$$\mathrm{log}_{{n}} \:{n}\:=\mathrm{1} \\ $$$$\mathrm{log}_{{x}+\mathrm{1}} \:\mathrm{2}\:+\mathrm{log}_{{x}+\mathrm{2}} \:\mathrm{3}\:+\mathrm{log}_{{x}+\mathrm{3}} \:\mathrm{4}\:=\mathrm{3} \\ $$$${x}+\mathrm{1}=\mathrm{2}\wedge{x}+\mathrm{2}=\mathrm{3}\wedge{x}+\mathrm{3}=\mathrm{4}\:\Rightarrow\:{x}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{3} \\ $$
Answered by MJS_new last updated on 15/Oct/20
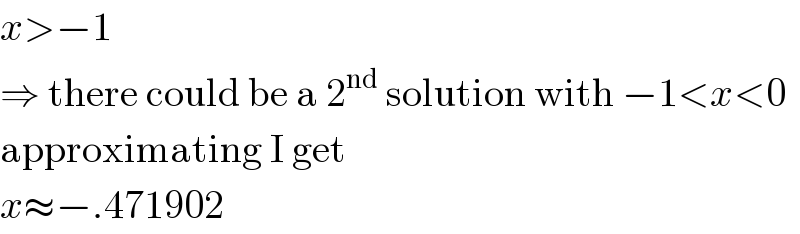
$${x}>−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{there}\:\mathrm{could}\:\mathrm{be}\:\mathrm{a}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution}\:\mathrm{with}\:−\mathrm{1}<{x}<\mathrm{0} \\ $$$$\mathrm{approximating}\:\mathrm{I}\:\mathrm{get} \\ $$$${x}\approx−.\mathrm{471902} \\ $$
