Question-118210

Question Number 118210 by bemath last updated on 16/Oct/20

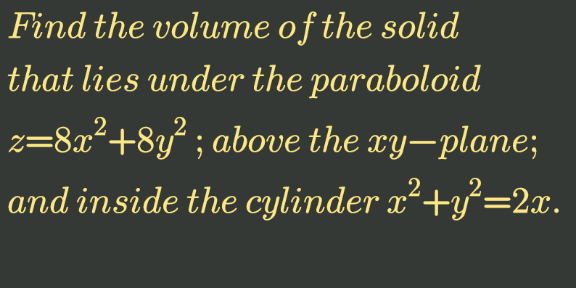
Answered by john santu last updated on 16/Oct/20

R e d u c e s t h e e q u a t i o n o f t h e c y l i n d e r

t o r^{2} = 2 r \cos θ o r r = 2 \cos θ, i n θ \in [0, π]

T h e v o l u m e e q u a l s

\int \int (8 x^{2} + 8 y^{2}) d A = \underset{0}{\int^{π}} \int_{0}^{2 \cos θ} (8 r^{2}) . (r d r d θ)

= \underset{0}{\int^{π}} (2 r^{4}) ∣_{0}^{2 \cos θ} d θ = \int_{0}^{π} 32 \cos^{4} θ d θ

= 32 \int_{0}^{π} {(\frac{1}{2} (1 + \cos 2 θ))}^{2} d θ

= 4 \underset{0}{\int^{π}} (3 + 4 \cos 2 θ + \cos (4 θ)) d θ

= 12 π