Question Number 118448 by peter frank last updated on 17/Oct/20

Answered by Olaf last updated on 17/Oct/20
![A = π×7^2 −2∫_(−7) ^(+7) (7−(√(49−x^2 )))dx A = 49π−4∫_0 ^(+7) (7−(√(49−x^2 )))dx A = 49π−196+28∫_0 ^(+7) ((√(1−((x/7))^2 )))dx x = 7sinθ A = 49π−196+28∫_0 ^(π/2) (cosθ)×7cosθdθ A = 49π−196+196∫_0 ^(π/2) ((1+cos2θ)/2)dθ A = 49π−196+98[θ+((sin2θ)/2)]_0 ^(π/2) A = 49π−196+98((π/2)) A = 98π−196](https://www.tinkutara.com/question/Q118451.png)
$$\mathrm{A}\:=\:\pi×\mathrm{7}^{\mathrm{2}} −\mathrm{2}\int_{−\mathrm{7}} ^{+\mathrm{7}} \left(\mathrm{7}−\sqrt{\mathrm{49}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{4}\int_{\mathrm{0}} ^{+\mathrm{7}} \left(\mathrm{7}−\sqrt{\mathrm{49}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{28}\int_{\mathrm{0}} ^{+\mathrm{7}} \left(\sqrt{\mathrm{1}−\left(\frac{{x}}{\mathrm{7}}\right)^{\mathrm{2}} }\right){dx} \\ $$$${x}\:=\:\mathrm{7sin}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{28}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cos}\theta\right)×\mathrm{7cos}\theta{d}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{196}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cos2}\theta}{\mathrm{2}}{d}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{98}\left[\theta+\frac{\mathrm{sin2}\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{98}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{98}\pi−\mathrm{196} \\ $$
Commented by peter frank last updated on 17/Oct/20

$$\mathrm{ans}\:\mathrm{33}.\mathrm{6}\:\mathrm{cm}^{\mathrm{2}} \\ $$
Answered by mr W last updated on 18/Oct/20

$${shaded}\:{area}={circle}−\mathrm{4}\:{segments} \\ $$$$\pi{R}^{\mathrm{2}} −\mathrm{4}×\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{3}}\right){R}^{\mathrm{2}} \\ $$$${with}\:{R}=\mathrm{7}\:{cm} \\ $$
Commented by peter frank last updated on 17/Oct/20

$$\mathrm{ans}\:\mathrm{33}.\mathrm{6cm}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 18/Oct/20

$${put}\:{R}=\mathrm{7},\:{you}\:{get}\:{answer}\:\mathrm{33}.\mathrm{558}\:{cm}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 18/Oct/20

$${it}\:{is}\:{meant}\:{that}\:{the}\:{radius}\:{of}\:{circle} \\ $$$${is}\:{equal}\:{the}\:{radius}\:{of}\:{segment}. \\ $$$${the}\:{diagram}\:{was}\:{just}\:{not}\:{well}\:{made}. \\ $$
Commented by peter frank last updated on 18/Oct/20

$$\mathrm{more}\:\mathrm{explanation}.\mathrm{i}\:\mathrm{did} \\ $$$$\mathrm{not}\:\mathrm{understood} \\ $$$$\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:? \\ $$
Commented by mr W last updated on 18/Oct/20

$${area}\:{of}\:{segment} \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right) \\ $$$${here}\:{we}\:{have}\:\theta=\mathrm{120}°=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$
Commented by mr W last updated on 18/Oct/20
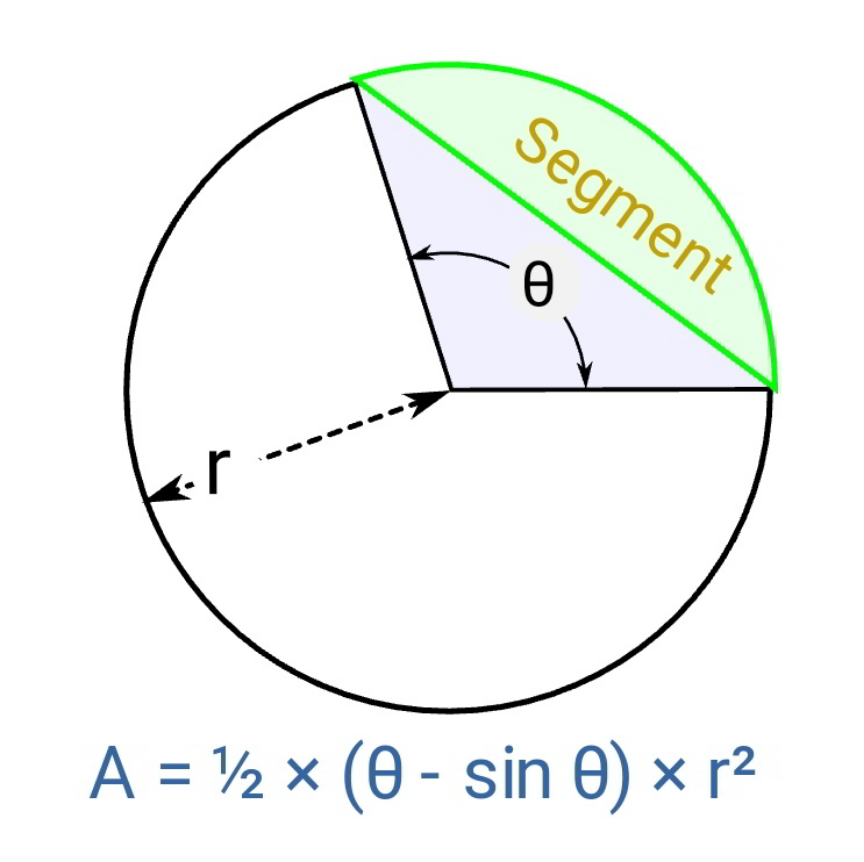
Commented by mr W last updated on 18/Oct/20

Commented by 1549442205PVT last updated on 18/Oct/20

$$\mathrm{But}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{R}.\mathrm{The}\:\mathrm{given} \\ $$$$\mathrm{segment}\:\mathrm{on}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{isn}'\mathrm{t}\:\mathrm{the}\:\mathrm{radius} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$
Commented by mr W last updated on 18/Oct/20

Commented by peter frank last updated on 18/Oct/20

Commented by peter frank last updated on 18/Oct/20

$$\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{diagram} \\ $$$$\mathrm{clear} \\ $$
Commented by peter frank last updated on 18/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by 1549442205PVT last updated on 18/Oct/20
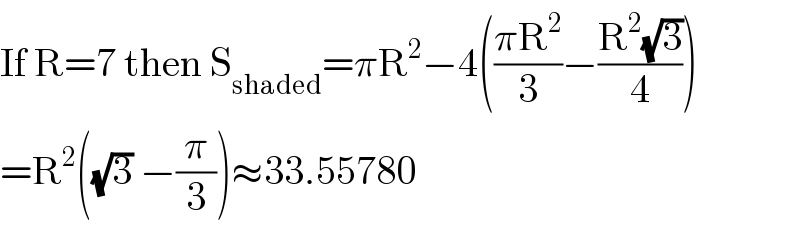
$$\mathrm{If}\:\mathrm{R}=\mathrm{7}\:\mathrm{then}\:\mathrm{S}_{\mathrm{shaded}} =\pi\mathrm{R}^{\mathrm{2}} −\mathrm{4}\left(\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\mathrm{R}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}\:−\frac{\pi}{\mathrm{3}}\right)\approx\mathrm{33}.\mathrm{55780} \\ $$
Commented by peter frank last updated on 18/Oct/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by 1549442205PVT last updated on 18/Oct/20

Commented by 1549442205PVT last updated on 18/Oct/20

$$\mathrm{This}\:\mathrm{problem}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{have}\:\mathrm{enough}\: \\ $$$$\mathrm{data}\:\mathrm{to}\:\mathrm{solve}.\mathrm{Indeed},\mathrm{we}\:\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{can}\:\mathrm{construct}\:\mathrm{many}\:\mathrm{the}\:\mathrm{figures} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{of}\:\mathrm{problem} \\ $$$$\mathrm{Put}\:\alpha=\widehat {\mathrm{ASQ}},\mathrm{R}−\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circles} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{centers}\:\mathrm{at}\:\left(\mathrm{A}\right)\:\mathrm{and}\:\left(\mathrm{C}\right).\mathrm{Then} \\ $$$$\mathrm{AQ}=\mathrm{2Rsin}\alpha,\mathrm{AO}=\mathrm{R}.\mathrm{Hence},\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have}\:\mathrm{PQ}\bot\mathrm{SN}\:\mathrm{at}\:\mathrm{A}\:\mathrm{and} \\ $$$$\mathrm{NP}=\mathrm{OQ}=\mathrm{7}.\mathrm{From}\:\mathrm{Pithagorean}'\mathrm{s} \\ $$$$\mathrm{theorem}\:\mathrm{we}\:\mathrm{have}:\mathrm{AQ}^{\mathrm{2}} +\mathrm{AO}^{\mathrm{2}} =\mathrm{OQ}^{\mathrm{2}} =\mathrm{49} \\ $$$$\Leftrightarrow\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{R}^{\mathrm{2}} =\mathrm{49}\Rightarrow\mathrm{R}=\frac{\mathrm{7}}{\:\sqrt{\mathrm{4sin}^{\mathrm{2}} \alpha+\mathrm{1}}} \\ $$$$\mathrm{or}\:\mathrm{sin}\alpha=\sqrt{\frac{\mathrm{49}−\mathrm{R}^{\mathrm{2}} }{\mathrm{4R}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{49}−\mathrm{R}^{\mathrm{2}} }}{\mathrm{2R}} \\ $$$$\mathrm{Therefore},\mathrm{for}\:\mathrm{each}\:\mathrm{of}\:\mathrm{valuesR}\:\mathrm{satisfying} \\ $$$$\mathrm{4}.\mathrm{95}\approx\frac{\mathrm{7}}{\:\sqrt{\mathrm{2}}}\leqslant\mathrm{R}<\mathrm{7}\:\mathrm{we}\:\mathrm{determine}\:\mathrm{one}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{angle}\:\alpha\:\mathrm{as}\:\mathrm{on}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{segments}\:\mathrm{NP}=\mathrm{OQ}=\mathrm{7}\:\mathrm{satisfying}\:\mathrm{the}\: \\ $$$$\mathrm{cionditions}\:\mathrm{of}\:\mathrm{given}\:\mathrm{problem}! \\ $$
