Question Number 118506 by meireza last updated on 18/Oct/20
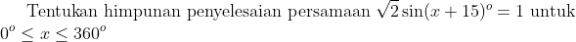
Answered by Lordose last updated on 18/Oct/20
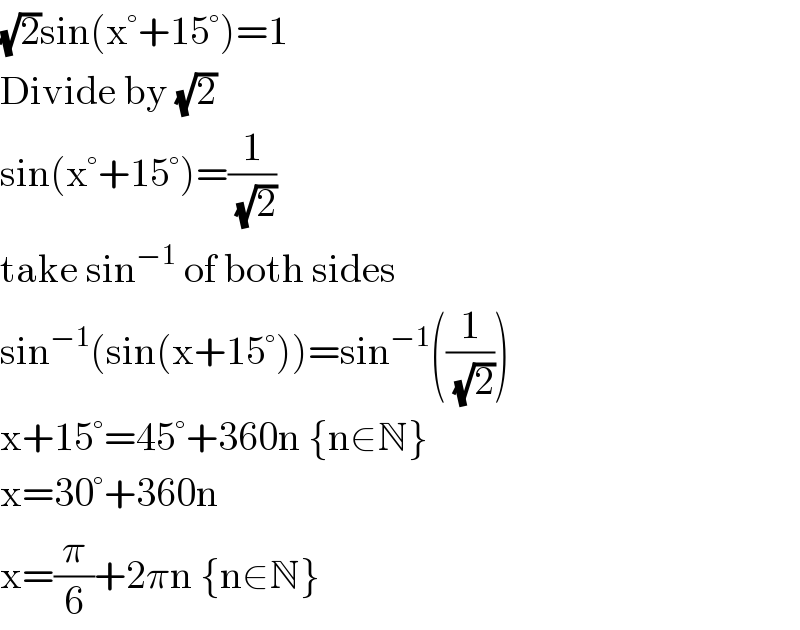
$$\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}°+\mathrm{15}°\right)=\mathrm{1} \\ $$$$\mathrm{Divide}\:\mathrm{by}\:\sqrt{\mathrm{2}} \\ $$$$\mathrm{sin}\left(\mathrm{x}°+\mathrm{15}°\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{take}\:\mathrm{sin}^{−\mathrm{1}} \:\mathrm{of}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\left(\mathrm{x}+\mathrm{15}°\right)\right)=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\mathrm{x}+\mathrm{15}°=\mathrm{45}°+\mathrm{360n}\:\left\{\mathrm{n}\in\mathbb{N}\right\} \\ $$$$\mathrm{x}=\mathrm{30}°+\mathrm{360n} \\ $$$$\mathrm{x}=\frac{\pi}{\mathrm{6}}+\mathrm{2}\pi\mathrm{n}\:\left\{\mathrm{n}\in\mathbb{N}\right\} \\ $$
Answered by ebi last updated on 18/Oct/20
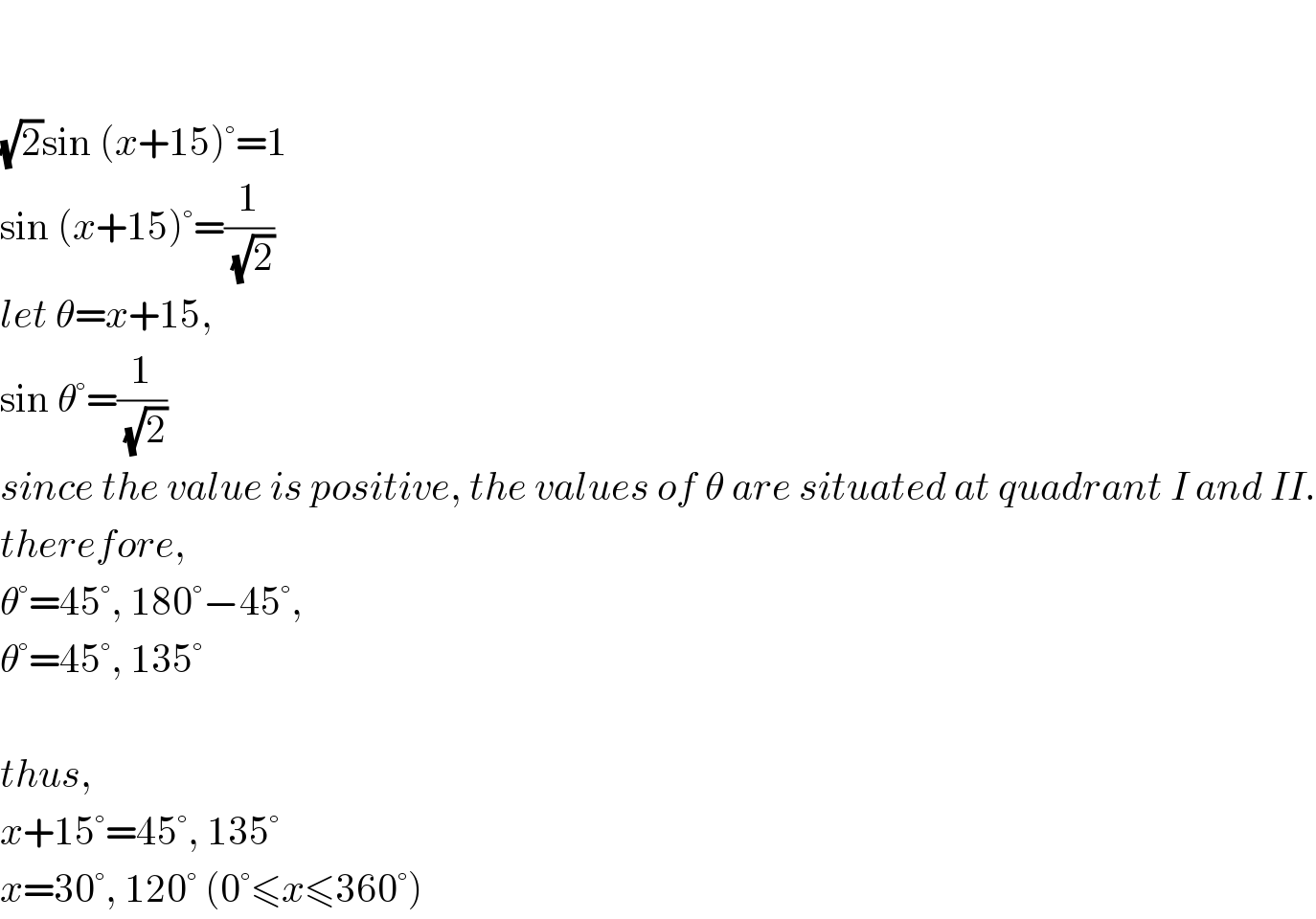
$$ \\ $$$$ \\ $$$$\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\mathrm{15}\right)°=\mathrm{1} \\ $$$$\mathrm{sin}\:\left({x}+\mathrm{15}\right)°=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${let}\:\theta={x}+\mathrm{15}, \\ $$$$\mathrm{sin}\:\theta°=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${since}\:{the}\:{value}\:{is}\:{positive},\:{the}\:{values}\:{of}\:\theta\:{are}\:{situated}\:{at}\:{quadrant}\:{I}\:{and}\:{II}. \\ $$$${therefore},\: \\ $$$$\theta°=\mathrm{45}°,\:\mathrm{180}°−\mathrm{45}°, \\ $$$$\theta°=\mathrm{45}°,\:\mathrm{135}° \\ $$$$ \\ $$$${thus}, \\ $$$${x}+\mathrm{15}°=\mathrm{45}°,\:\mathrm{135}° \\ $$$${x}=\mathrm{30}°,\:\mathrm{120}°\:\left(\mathrm{0}°\leqslant{x}\leqslant\mathrm{360}°\right) \\ $$
