Menu Close

Question-118690

Tinku Tara 0 Comments
Pin




Question Number 118690 by Algoritm last updated on 19/Oct/20
Answered by benjo_mathlover last updated on 19/Oct/20
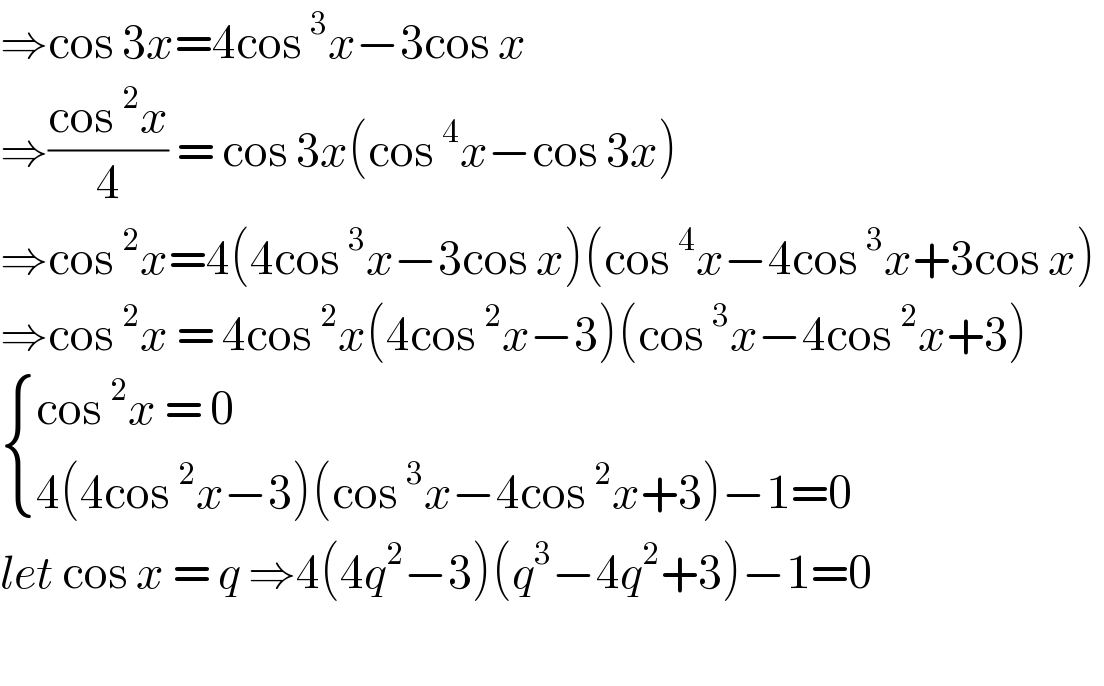
⇒cos 3x=4cos^3 x−3cos x ⇒((cos^2 x)/4) = cos 3x(cos^4 x−cos 3x) ⇒cos^2 x=4(4cos^3 x−3cos x)(cos^4 x−4cos^3 x+3cos x) ⇒cos^2 x = 4cos^2 x(4cos^2 x−3)(cos^3 x−4cos^2 x+3) { ((cos^2 x = 0)),((4(4cos^2 x−3)(cos^3 x−4cos^2 x+3)−1=0)) :} let cos x = q ⇒4(4q^2 −3)(q^3 −4q^2 +3)−1=0
$$\Rightarrow\mathrm{cos}\:\mathrm{3}{x}=\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{4}}\:=\:\mathrm{cos}\:\mathrm{3}{x}\left(\mathrm{cos}\:^{\mathrm{4}} {x}−\mathrm{cos}\:\mathrm{3}{x}\right) \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} {x}=\mathrm{4}\left(\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}\right)\left(\mathrm{cos}\:^{\mathrm{4}} {x}−\mathrm{4cos}\:^{\mathrm{3}} {x}+\mathrm{3cos}\:{x}\right)\: \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} {x}\:=\:\mathrm{4cos}\:^{\mathrm{2}} {x}\left(\mathrm{4cos}\:^{\mathrm{2}} {x}−\mathrm{3}\right)\left(\mathrm{cos}\:^{\mathrm{3}} {x}−\mathrm{4cos}\:^{\mathrm{2}} {x}+\mathrm{3}\right) \\ $$$$\begin{cases}{\mathrm{cos}\:^{\mathrm{2}} {x}\:=\:\mathrm{0}}\\{\mathrm{4}\left(\mathrm{4cos}\:^{\mathrm{2}} {x}−\mathrm{3}\right)\left(\mathrm{cos}\:^{\mathrm{3}} {x}−\mathrm{4cos}\:^{\mathrm{2}} {x}+\mathrm{3}\right)−\mathrm{1}=\mathrm{0}}\end{cases} \\ $$$${let}\:\mathrm{cos}\:{x}\:=\:{q}\:\Rightarrow\mathrm{4}\left(\mathrm{4}{q}^{\mathrm{2}} −\mathrm{3}\right)\left({q}^{\mathrm{3}} −\mathrm{4}{q}^{\mathrm{2}} +\mathrm{3}\right)−\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 19/Oct/20
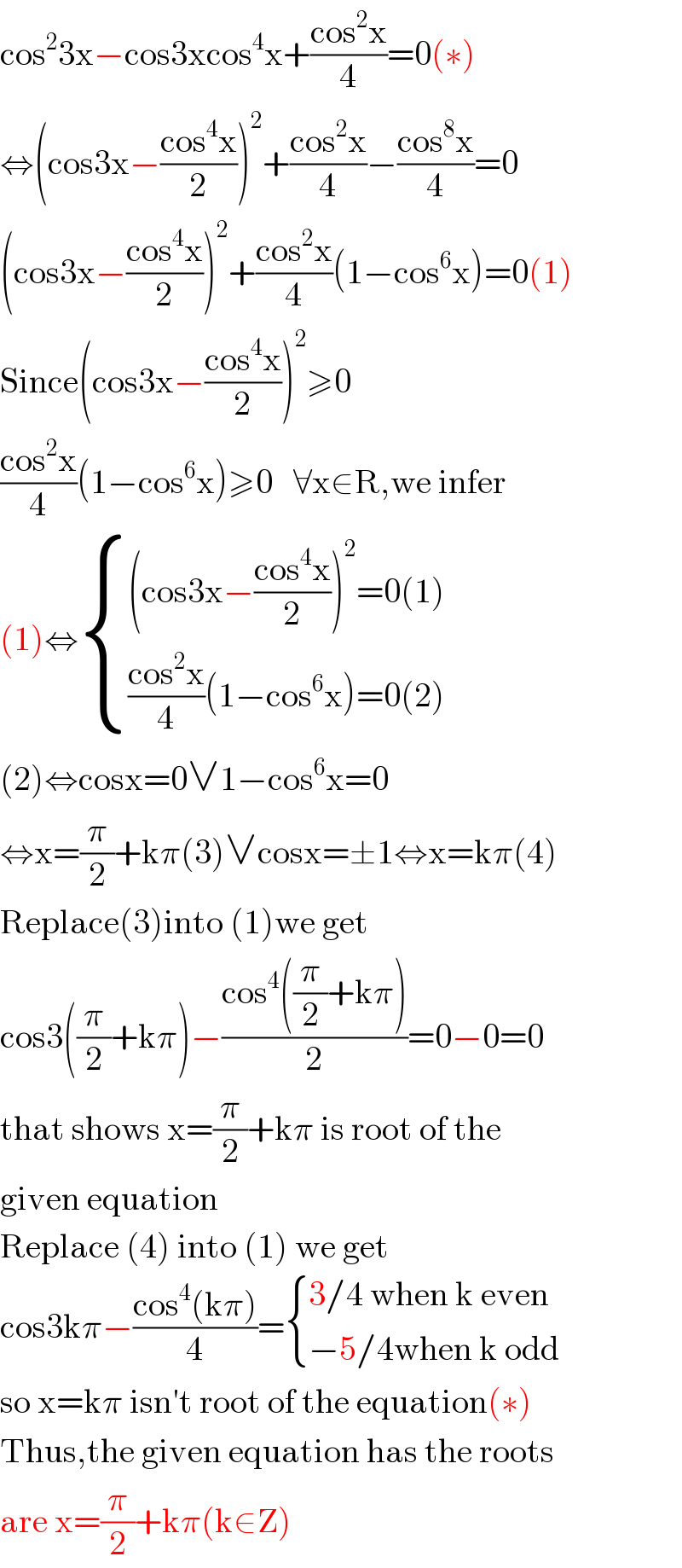
cos^2 3x−cos3xcos^4 x+((cos^2 x)/4)=0(∗) ⇔(cos3x−((cos^4 x)/2))^2 +((cos^2 x)/4)−((cos^8 x)/4)=0 (cos3x−((cos^4 x)/2))^2 +((cos^2 x)/4)(1−cos^6 x)=0(1) Since(cos3x−((cos^4 x)/2))^2 ≥0 ((cos^2 x)/4)(1−cos^6 x)≥0 ∀x∈R,we infer (1)⇔ { (((cos3x−((cos^4 x)/2))^2 =0(1))),((((cos^2 x)/4)(1−cos^6 x)=0(2))) :} (2)⇔cosx=0∨1−cos^6 x=0 ⇔x=(π/2)+kπ(3)∨cosx=±1⇔x=kπ(4) Replace(3)into (1)we get cos3((π/2)+kπ)−((cos^4 ((π/2)+kπ))/2)=0−0=0 that shows x=(π/2)+kπ is root of the given equation Replace (4) into (1) we get cos3kπ−((cos^4 (kπ))/4)= { ((3/4 when k even)),((−5/4when k odd)) :} so x=kπ isn′t root of the equation(∗) Thus,the given equation has the roots are x=(π/2)+kπ(k∈Z)
$$\mathrm{cos}^{\mathrm{2}} \mathrm{3x}−\mathrm{cos3xcos}^{\mathrm{4}} \mathrm{x}+\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{4}}=\mathrm{0}\left(\ast\right) \\ $$$$\Leftrightarrow\left(\mathrm{cos3x}−\frac{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{4}}−\frac{\mathrm{cos}^{\mathrm{8}} \mathrm{x}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left(\mathrm{cos3x}−\frac{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{6}} \mathrm{x}\right)=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{Since}\left(\mathrm{cos3x}−\frac{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{6}} \mathrm{x}\right)\geqslant\mathrm{0}\:\:\:\forall\mathrm{x}\in\mathrm{R},\mathrm{we}\:\mathrm{infer} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\begin{cases}{\left(\mathrm{cos3x}−\frac{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0}\left(\mathrm{1}\right)}\\{\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{6}} \mathrm{x}\right)=\mathrm{0}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{cosx}=\mathrm{0}\vee\mathrm{1}−\mathrm{cos}^{\mathrm{6}} \mathrm{x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\left(\mathrm{3}\right)\vee\mathrm{cosx}=\pm\mathrm{1}\Leftrightarrow\mathrm{x}=\mathrm{k}\pi\left(\mathrm{4}\right) \\ $$$$\mathrm{Replace}\left(\mathrm{3}\right)\mathrm{into}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{cos3}\left(\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\right)−\frac{\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\right)}{\mathrm{2}}=\mathrm{0}−\mathrm{0}=\mathrm{0} \\ $$$$\mathrm{that}\:\mathrm{shows}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{Replace}\:\left(\mathrm{4}\right)\:\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{cos3k}\pi−\frac{\mathrm{cos}^{\mathrm{4}} \left(\mathrm{k}\pi\right)}{\mathrm{4}}=\begin{cases}{\mathrm{3}/\mathrm{4}\:\mathrm{when}\:\mathrm{k}\:\mathrm{even}}\\{−\mathrm{5}/\mathrm{4when}\:\mathrm{k}\:\mathrm{odd}}\end{cases} \\ $$$$\mathrm{so}\:\mathrm{x}=\mathrm{k}\pi\:\mathrm{isn}'\mathrm{t}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\left(\ast\right) \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{the}\:\mathrm{roots} \\ $$$$\mathrm{are}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\left(\mathrm{k}\in\mathrm{Z}\right) \\ $$
Commented by bemath last updated on 19/Oct/20
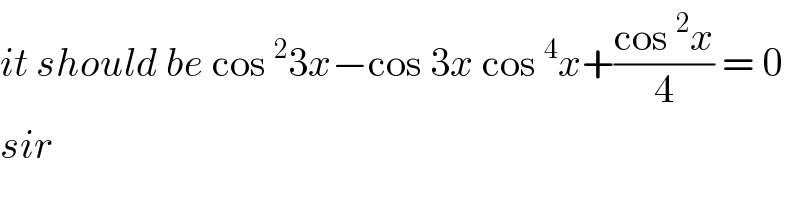
it should be cos^2 3x−cos 3x cos^4 x+((cos^2 x)/4) = 0 sir
$${it}\:{should}\:{be}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{x}−\mathrm{cos}\:\mathrm{3}{x}\:\mathrm{cos}\:^{\mathrm{4}} {x}+\frac{\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{4}}\:=\:\mathrm{0} \\ $$$${sir} \\ $$
Commented by 1549442205PVT last updated on 19/Oct/20
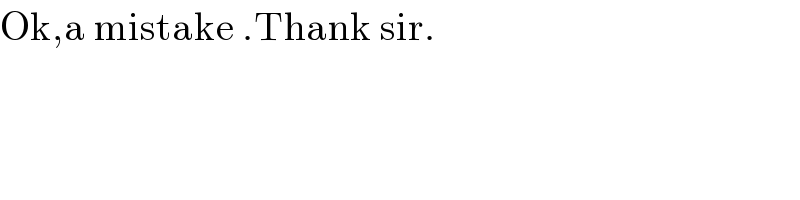
Ok,a mistake .Thank sir.
$$\mathrm{Ok},\mathrm{a}\:\mathrm{mistake}\:.\mathrm{Thank}\:\mathrm{sir}. \\ $$
Answered by MJS_new last updated on 19/Oct/20
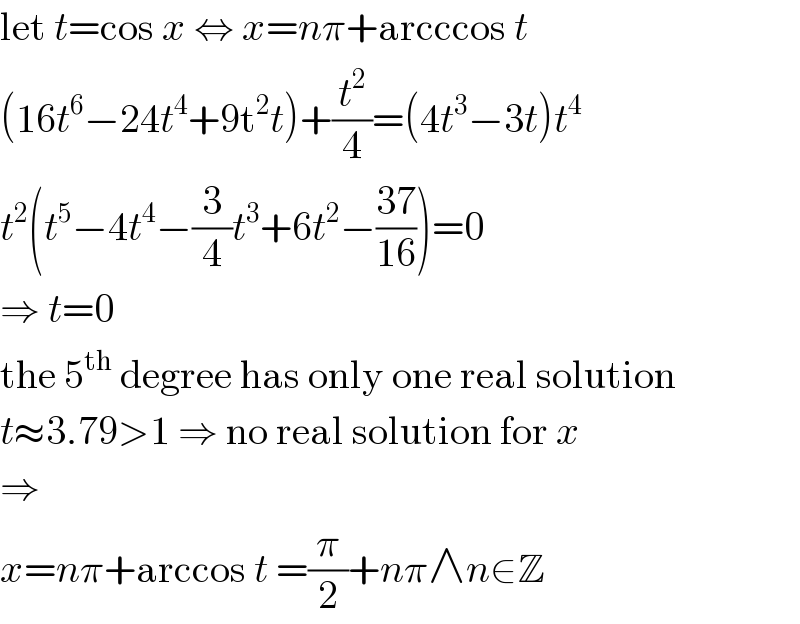
let t=cos x ⇔ x=nπ+arcccos t (16t^6 −24t^4 +9t^2 t)+(t^2 /4)=(4t^3 −3t)t^4 t^2 (t^5 −4t^4 −(3/4)t^3 +6t^2 −((37)/(16)))=0 ⇒ t=0 the 5^(th) degree has only one real solution t≈3.79>1 ⇒ no real solution for x ⇒ x=nπ+arccos t =(π/2)+nπ∧n∈Z
$$\mathrm{let}\:{t}=\mathrm{cos}\:{x}\:\Leftrightarrow\:{x}={n}\pi+\mathrm{arcccos}\:{t} \\ $$$$\left(\mathrm{16}{t}^{\mathrm{6}} −\mathrm{24}{t}^{\mathrm{4}} +\mathrm{9t}^{\mathrm{2}} {t}\right)+\frac{{t}^{\mathrm{2}} }{\mathrm{4}}=\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{3}{t}\right){t}^{\mathrm{4}} \\ $$$${t}^{\mathrm{2}} \left({t}^{\mathrm{5}} −\mathrm{4}{t}^{\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{4}}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} −\frac{\mathrm{37}}{\mathrm{16}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{5}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{has}\:\mathrm{only}\:\mathrm{one}\:\mathrm{real}\:\mathrm{solution} \\ $$$${t}\approx\mathrm{3}.\mathrm{79}>\mathrm{1}\:\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for}\:{x} \\ $$$$\Rightarrow \\ $$$${x}={n}\pi+\mathrm{arccos}\:{t}\:=\frac{\pi}{\mathrm{2}}+{n}\pi\wedge{n}\in\mathbb{Z} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *