Question Number 118768 by mathdave last updated on 19/Oct/20
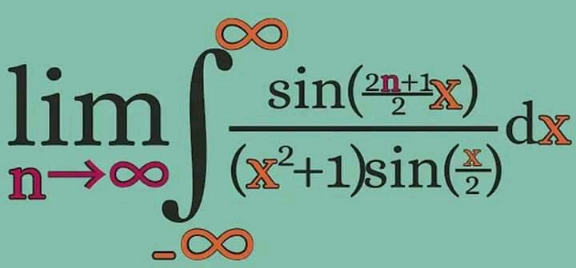
Answered by mindispower last updated on 23/Oct/20
![Σ_(m=0) ^n e^(imx) =((1−(e^(ix) )^(n+1) )/(1−e^(ix) ))=((e^(i((nx)/2)) (e^(−i(((n+1)x)/2)) −e^(i(((n+1)x)/2)) ))/(e^(−i(x/2)) −e^(i(x/2)) )) =e^(i((nx)/2)) .((sin(((n+1)/2)x))/(sin((x/2)))) ⇒((sin(((2n+1)/2)x))/(sin((x/2))))=e^(−inx) Σ_(m=0) ^(2n) e^(imx) ∫_(−∞) ^∞ ((e^(ikx) )/(1+x^2 ))dx ,k≥0 C_R ={Re^(ia) ,a∈[0,π]} ∫_C_R (e^(ikx) /(1+x^2 ))dx=∫_(−∞) ^∞ (e^(ikx) /(1+x^2 ))dx+∫_0 ^π ((iRe^(−ksin(x)) dx)/(1+R^2 e^(2ix) )) =2iπ.(e^(−k) /(2i))=(π/e^k ), ⇒Σ_(m≤2n) (π/e^(∣m−n∣) )=Σ_(m≤n) (π/e^(n−m) )+Σ_(m>n) (π/e^(m−n) ) =(π/e^n )(((1−e^((n+1)) )/(1−e)))+πe^n (e^(−(n+1)) (((1−e^(−(n)) )/(1−e^(−1) )))) lim n→0 =−((πe)/(1−e))+πe^(−1) .(1/(1−e^− )) =(π/(e−1))(e+1)=π(((e^(1/2) /2)+(e^(−(1/2)) /2) )/((1/2)(e^(1/2) −e^(−(1/2)) )))=πcoth((1/2))](https://www.tinkutara.com/question/Q119274.png)
$$\underset{{m}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{imx}} =\frac{\mathrm{1}−\left({e}^{{ix}} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−{e}^{{ix}} }=\frac{{e}^{{i}\frac{{nx}}{\mathrm{2}}} \left({e}^{−{i}\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}} −{e}^{{i}\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}} \right)}{{e}^{−{i}\frac{{x}}{\mathrm{2}}} −{e}^{{i}\frac{{x}}{\mathrm{2}}} } \\ $$$$={e}^{{i}\frac{{nx}}{\mathrm{2}}} .\frac{{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\frac{{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}={e}^{−{inx}} \underset{{m}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{e}^{{imx}} \\ $$$$\int_{−\infty} ^{\infty} \frac{{e}^{{ikx}} \:}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:,{k}\geqslant\mathrm{0} \\ $$$${C}_{{R}} =\left\{{Re}^{{ia}} ,{a}\in\left[\mathrm{0},\pi\right]\right\} \\ $$$$\int_{{C}_{{R}} } \frac{{e}^{{ikx}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{−\infty} ^{\infty} \frac{{e}^{{ikx}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{0}} ^{\pi} \frac{{iRe}^{−{ksin}\left({x}\right)} {dx}}{\mathrm{1}+{R}^{\mathrm{2}} {e}^{\mathrm{2}{ix}} } \\ $$$$=\mathrm{2}{i}\pi.\frac{{e}^{−{k}} }{\mathrm{2}{i}}=\frac{\pi}{{e}^{{k}} }, \\ $$$$\Rightarrow\underset{{m}\leqslant\mathrm{2}{n}} {\sum}\frac{\pi}{{e}^{\mid{m}−{n}\mid} }=\underset{{m}\leqslant{n}} {\sum}\frac{\pi}{{e}^{{n}−{m}} }+\underset{{m}>{n}} {\sum}\frac{\pi}{{e}^{{m}−{n}} } \\ $$$$=\frac{\pi}{{e}^{{n}} }\left(\frac{\mathrm{1}−{e}^{\left({n}+\mathrm{1}\right)} }{\mathrm{1}−{e}}\right)+\pi{e}^{{n}} \left({e}^{−\left({n}+\mathrm{1}\right)} \left(\frac{\mathrm{1}−{e}^{−\left({n}\right)} }{\mathrm{1}−{e}^{−\mathrm{1}} }\right)\right) \\ $$$${lim}\:{n}\rightarrow\mathrm{0} \\ $$$$=−\frac{\pi{e}}{\mathrm{1}−{e}}+\pi{e}^{−\mathrm{1}} .\frac{\mathrm{1}}{\mathrm{1}−{e}^{−} } \\ $$$$=\frac{\pi}{{e}−\mathrm{1}}\left({e}+\mathrm{1}\right)=\pi\frac{\frac{{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}}+\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}}\:}{\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\frac{\mathrm{1}}{\mathrm{2}}} −{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)}=\pi{coth}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
