Question Number 118849 by mr W last updated on 20/Oct/20
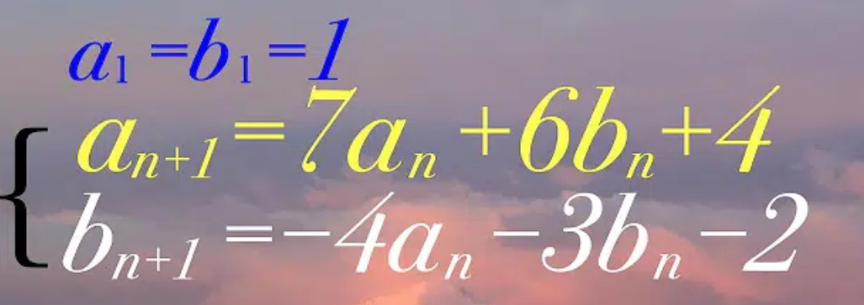
Commented by PRITHWISH SEN 2 last updated on 20/Oct/20

$$\left(\mathrm{a}_{\mathrm{n}} +\mathrm{b}_{\mathrm{n}} \right)=\:\mathrm{3}^{\mathrm{n}} −\mathrm{1} \\ $$
Commented by mr W last updated on 20/Oct/20
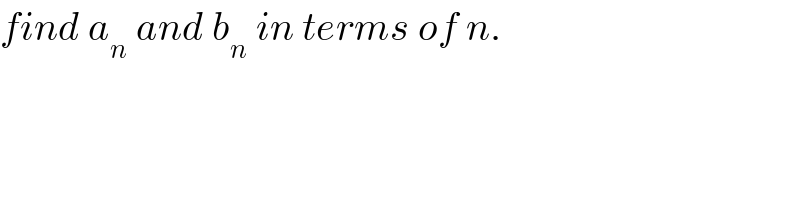
$${find}\:{a}_{{n}} \:{and}\:{b}_{{n}} \:{in}\:{terms}\:{of}\:{n}. \\ $$
Answered by mr W last updated on 20/Oct/20
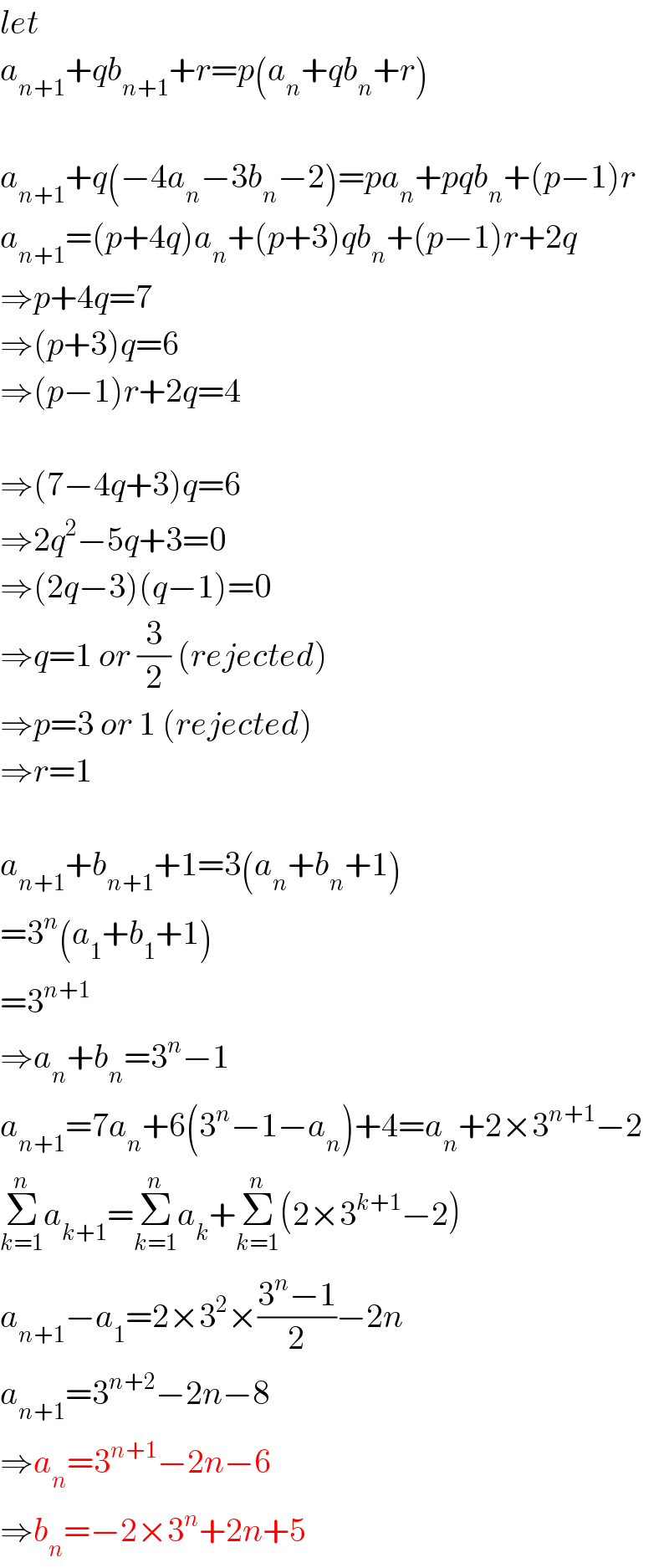
$${let} \\ $$$${a}_{{n}+\mathrm{1}} +{qb}_{{n}+\mathrm{1}} +{r}={p}\left({a}_{{n}} +{qb}_{{n}} +{r}\right) \\ $$$$ \\ $$$${a}_{{n}+\mathrm{1}} +{q}\left(−\mathrm{4}{a}_{{n}} −\mathrm{3}{b}_{{n}} −\mathrm{2}\right)={pa}_{{n}} +{pqb}_{{n}} +\left({p}−\mathrm{1}\right){r} \\ $$$${a}_{{n}+\mathrm{1}} =\left({p}+\mathrm{4}{q}\right){a}_{{n}} +\left({p}+\mathrm{3}\right){qb}_{{n}} +\left({p}−\mathrm{1}\right){r}+\mathrm{2}{q} \\ $$$$\Rightarrow{p}+\mathrm{4}{q}=\mathrm{7} \\ $$$$\Rightarrow\left({p}+\mathrm{3}\right){q}=\mathrm{6} \\ $$$$\Rightarrow\left({p}−\mathrm{1}\right){r}+\mathrm{2}{q}=\mathrm{4} \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{7}−\mathrm{4}{q}+\mathrm{3}\right){q}=\mathrm{6} \\ $$$$\Rightarrow\mathrm{2}{q}^{\mathrm{2}} −\mathrm{5}{q}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{q}−\mathrm{3}\right)\left({q}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{q}=\mathrm{1}\:{or}\:\frac{\mathrm{3}}{\mathrm{2}}\:\left({rejected}\right) \\ $$$$\Rightarrow{p}=\mathrm{3}\:{or}\:\mathrm{1}\:\left({rejected}\right) \\ $$$$\Rightarrow{r}=\mathrm{1}\: \\ $$$$ \\ $$$${a}_{{n}+\mathrm{1}} +{b}_{{n}+\mathrm{1}} +\mathrm{1}=\mathrm{3}\left({a}_{{n}} +{b}_{{n}} +\mathrm{1}\right) \\ $$$$=\mathrm{3}^{{n}} \left({a}_{\mathrm{1}} +{b}_{\mathrm{1}} +\mathrm{1}\right) \\ $$$$=\mathrm{3}^{{n}+\mathrm{1}} \\ $$$$\Rightarrow{a}_{{n}} +{b}_{{n}} =\mathrm{3}^{{n}} −\mathrm{1} \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{7}{a}_{{n}} +\mathrm{6}\left(\mathrm{3}^{{n}} −\mathrm{1}−{a}_{{n}} \right)+\mathrm{4}={a}_{{n}} +\mathrm{2}×\mathrm{3}^{{n}+\mathrm{1}} −\mathrm{2} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}+\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}×\mathrm{3}^{{k}+\mathrm{1}} −\mathrm{2}\right) \\ $$$${a}_{{n}+\mathrm{1}} −{a}_{\mathrm{1}} =\mathrm{2}×\mathrm{3}^{\mathrm{2}} ×\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{2}}−\mathrm{2}{n} \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}{n}−\mathrm{8} \\ $$$$\Rightarrow{a}_{{n}} =\mathrm{3}^{{n}+\mathrm{1}} −\mathrm{2}{n}−\mathrm{6} \\ $$$$\Rightarrow{b}_{{n}} =−\mathrm{2}×\mathrm{3}^{{n}} +\mathrm{2}{n}+\mathrm{5} \\ $$
Commented by PRITHWISH SEN 2 last updated on 21/Oct/20

$$\mathrm{excellent}\:\mathrm{sir} \\ $$
