Menu Close

Question-118872

Tinku Tara 0 Comments
Pin




Question Number 118872 by ZiYangLee last updated on 20/Oct/20
Commented by ZiYangLee last updated on 20/Oct/20
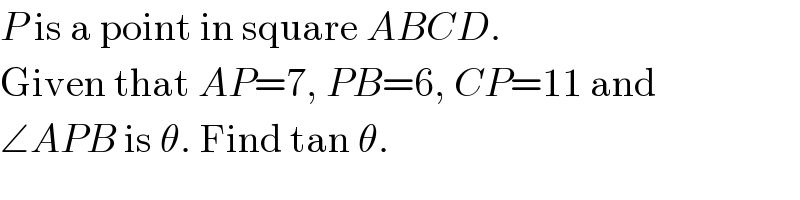
P is a point in square ABCD. Given that AP=7, PB=6, CP=11 and ∠APB is θ. Find tan θ.
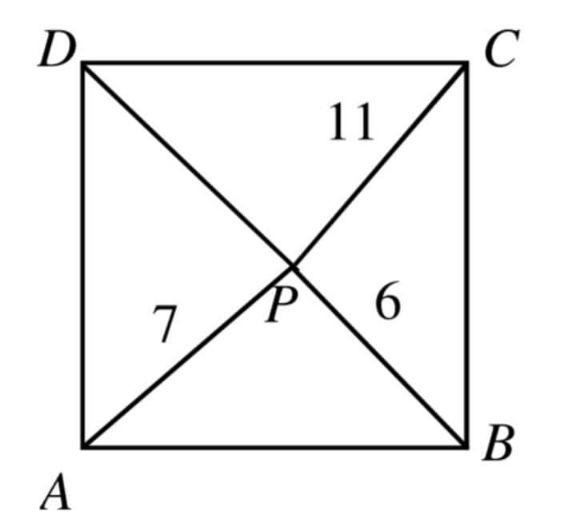
$${P}\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{in}\:\mathrm{square}\:{ABCD}.\: \\ $$$$\mathrm{Given}\:\mathrm{that}\:{AP}=\mathrm{7},\:{PB}=\mathrm{6},\:{CP}=\mathrm{11}\:\mathrm{and} \\ $$$$\angle{APB}\:\mathrm{is}\:\theta.\:\mathrm{Find}\:\mathrm{tan}\:\theta. \\ $$
Answered by 1549442205PVT last updated on 20/Oct/20
Commented by 1549442205PVT last updated on 21/Oct/20
Given AE=7,BE=6,CE=11.Denote ECF^(�) =α,EBF^(�) =β,AB=BC=a.Then CF=11cosα,BF=6cosβ.BG=EF=6sinβ AG=(√(AE^2 −EG^2 ))=(√(AE^2 −BF^2 )) =(√(49−36cos^2 β)) AG+BG=BF+CF=a.Therefore, (√(49−36cos^2 β)) +6sinβ=6cosβ+11cosα(∗) On the other hand,EF=11sinα=6sinβ ⇒sinα=((6sinβ)/(11))⇒sin^2 α=((36sin^2 β)/(121)) cosα=((√(121−36sin^2 β))/(11)).Replace into (∗) we get (√(49−36cos^2 β))+6sinβ=6cosβ+(√(121−36sin^2 β)) (√(49−36cos^2 β)) −(√(121−36sin^2 β)) =6cosβ−6sinβ Squaring two sides we get 170−36−2(√((49−36cos^2 β)(121−36sin^2 β))) =36−72sinβcosβ.Note sin2β=2sinβcosβ 49+18sin2β=(√(5929−36(121cos^2 β+49sin^2 β)+324sin^2 2β)) Squaring two sides again we get 2401+1764sin2β+324sin^2 2β= 5929−36.49−36.72cos^2 β+324sin^2 2β ⇔1764−2592cos^2 β=1764sin2β⇔ 468−1296cos2β=1764sin2β(since 2cos^2 β=1+cos2β) ⇔13=36cos2β+49sin2β.Put t=tanβ we have 36((1−t^2 )/(1+t^2 ))+49((2t)/(1+t^2 ))=13 ⇔36t^2 −98t−36+13t^2 +13=0 ⇔49t^2 −98t−23=0 Δ′=49^2 +49.23=49.72=(7.6(√2) )^2 t=tanβ=((49+42(√2))/(49))=((7+6(√2))/7)⇒β≈65°40′30 cosβ=(1/( (√(1+tan^2 β))))=(7/( (√(170+84(√2))))), ,EG=6cosβ=((42)/( (√(170+84(√2)))))(1) Put BEG^(�) =θ_1 ,AEG^(�) =θ_2 .Then we have tanθ_1 =((BG)/(EG))=((√(36−EG^2 ))/(EG))=(√(((36)/(EG^2 ))−1)) tanθ_2 =((AG)/(EG))=((√(49−EG^2 ))/(EG))=(√(((49)/(EG^2 ))−1)) From that and (1) we get tanθ=tan(θ_1 +θ_2 )=((tanθ_1 +tanθ_2 )/(1−tanθ_1 tanθ_2 )) =(((√(((36)/x^2 )−1))+(√(((49)/x^2 )−1)))/(1−(√((((36)/x^2 )−1)((√(((49)/x^2 )−1))))))) tanθ=((x((√(36−x^2 ))+(√(49−x^2 ))))/(x^2 −(√((36−x^2 )(49−x^2 ))))) ,x=EG We find out tan𝛉=−1 ⇒𝛉=135°
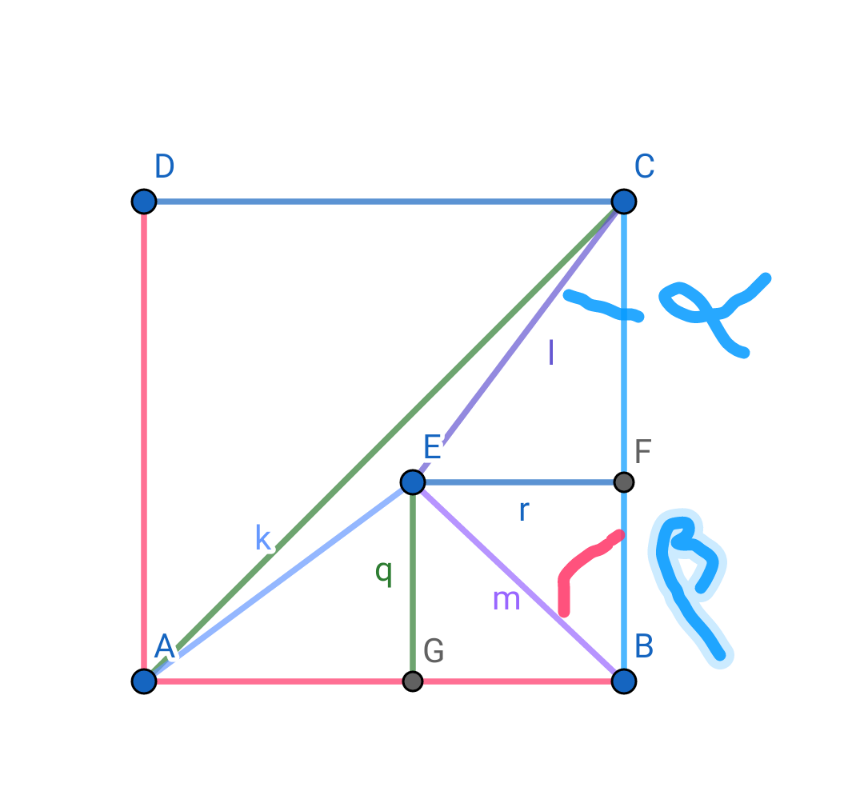
$$\mathrm{Given}\:\mathrm{AE}=\mathrm{7},\mathrm{BE}=\mathrm{6},\mathrm{CE}=\mathrm{11}.\mathrm{Denote} \\ $$$$\widehat {\mathrm{ECF}}=\alpha,\widehat {\mathrm{EBF}}=\beta,\mathrm{AB}=\mathrm{BC}=\mathrm{a}.\mathrm{Then} \\ $$$$\mathrm{CF}=\mathrm{11cos}\alpha,\mathrm{BF}=\mathrm{6cos}\beta.\mathrm{BG}=\mathrm{EF}=\mathrm{6sin}\beta \\ $$$$\mathrm{AG}=\sqrt{\mathrm{AE}^{\mathrm{2}} −\mathrm{EG}^{\mathrm{2}} }=\sqrt{\mathrm{AE}^{\mathrm{2}} −\mathrm{BF}^{\mathrm{2}} }\: \\ $$$$=\sqrt{\mathrm{49}−\mathrm{36cos}^{\mathrm{2}} \beta} \\ $$$$\mathrm{AG}+\mathrm{BG}=\mathrm{BF}+\mathrm{CF}=\mathrm{a}.\mathrm{Therefore}, \\ $$$$\sqrt{\mathrm{49}−\mathrm{36cos}^{\mathrm{2}} \beta}\:+\mathrm{6sin}\beta=\mathrm{6cos}\beta+\mathrm{11cos}\alpha\left(\ast\right) \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand},\mathrm{EF}=\mathrm{11sin}\alpha=\mathrm{6sin}\beta \\ $$$$\Rightarrow\mathrm{sin}\alpha=\frac{\mathrm{6sin}\beta}{\mathrm{11}}\Rightarrow\mathrm{sin}^{\mathrm{2}} \alpha=\frac{\mathrm{36sin}^{\mathrm{2}} \beta}{\mathrm{121}} \\ $$$$\mathrm{cos}\alpha=\frac{\sqrt{\mathrm{121}−\mathrm{36sin}^{\mathrm{2}} \beta}}{\mathrm{11}}.\mathrm{Replace}\:\mathrm{into}\:\left(\ast\right) \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{49}−\mathrm{36cos}^{\mathrm{2}} \beta}+\mathrm{6sin}\beta=\mathrm{6cos}\beta+\sqrt{\mathrm{121}−\mathrm{36sin}^{\mathrm{2}} \beta} \\ $$$$\sqrt{\mathrm{49}−\mathrm{36cos}^{\mathrm{2}} \beta}\:−\sqrt{\mathrm{121}−\mathrm{36sin}^{\mathrm{2}} \beta}\:=\mathrm{6cos}\beta−\mathrm{6sin}\beta \\ $$$$\mathrm{Squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{170}−\mathrm{36}−\mathrm{2}\sqrt{\left(\mathrm{49}−\mathrm{36cos}^{\mathrm{2}} \beta\right)\left(\mathrm{121}−\mathrm{36sin}^{\mathrm{2}} \beta\right)} \\ $$$$=\mathrm{36}−\mathrm{72sin}\beta\mathrm{cos}\beta.\mathrm{Note}\:\mathrm{sin2}\beta=\mathrm{2sin}\beta\mathrm{cos}\beta \\ $$$$\mathrm{49}+\mathrm{18sin2}\beta=\sqrt{\mathrm{5929}−\mathrm{36}\left(\mathrm{121cos}^{\mathrm{2}} \beta+\mathrm{49sin}^{\mathrm{2}} \beta\right)+\mathrm{324sin}^{\mathrm{2}} \mathrm{2}\beta} \\ $$$$\mathrm{Squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{again}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{2401}+\mathrm{1764sin2}\beta+\mathrm{324sin}^{\mathrm{2}} \mathrm{2}\beta= \\ $$$$\mathrm{5929}−\mathrm{36}.\mathrm{49}−\mathrm{36}.\mathrm{72cos}^{\mathrm{2}} \beta+\mathrm{324sin}^{\mathrm{2}} \mathrm{2}\beta \\ $$$$\Leftrightarrow\mathrm{1764}−\mathrm{2592cos}^{\mathrm{2}} \beta=\mathrm{1764sin2}\beta\Leftrightarrow \\ $$$$\mathrm{468}−\mathrm{1296cos2}\beta=\mathrm{1764sin2}\beta\left(\mathrm{since}\:\mathrm{2cos}^{\mathrm{2}} \beta=\mathrm{1}+\mathrm{cos2}\beta\right) \\ $$$$\Leftrightarrow\mathrm{13}=\mathrm{36cos2}\beta+\mathrm{49sin2}\beta.\mathrm{Put}\:\mathrm{t}=\mathrm{tan}\beta \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{36}\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\mathrm{49}\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\mathrm{13} \\ $$$$\Leftrightarrow\mathrm{36t}^{\mathrm{2}} −\mathrm{98t}−\mathrm{36}+\mathrm{13t}^{\mathrm{2}} +\mathrm{13}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{49t}^{\mathrm{2}} −\mathrm{98t}−\mathrm{23}=\mathrm{0} \\ $$$$\Delta'=\mathrm{49}^{\mathrm{2}} +\mathrm{49}.\mathrm{23}=\mathrm{49}.\mathrm{72}=\left(\mathrm{7}.\mathrm{6}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} \\ $$$$\mathrm{t}=\mathrm{tan}\beta=\frac{\mathrm{49}+\mathrm{42}\sqrt{\mathrm{2}}}{\mathrm{49}}=\frac{\mathrm{7}+\mathrm{6}\sqrt{\mathrm{2}}}{\mathrm{7}}\Rightarrow\beta\approx\mathrm{65}°\mathrm{40}'\mathrm{30} \\ $$$$\mathrm{cos}\beta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \beta}}=\frac{\mathrm{7}}{\:\sqrt{\mathrm{170}+\mathrm{84}\sqrt{\mathrm{2}}}}, \\ $$$$,\mathrm{EG}=\mathrm{6cos}\beta=\frac{\mathrm{42}}{\:\sqrt{\mathrm{170}+\mathrm{84}\sqrt{\mathrm{2}}}}\left(\mathrm{1}\right) \\ $$$$\mathrm{Put}\:\widehat {\mathrm{BEG}}=\theta_{\mathrm{1}} ,\widehat {\mathrm{AEG}}=\theta_{\mathrm{2}} .\mathrm{Then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{tan}\theta_{\mathrm{1}} =\frac{\mathrm{BG}}{\mathrm{EG}}=\frac{\sqrt{\mathrm{36}−\mathrm{EG}^{\mathrm{2}} }}{\mathrm{EG}}=\sqrt{\frac{\mathrm{36}}{\mathrm{EG}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\mathrm{tan}\theta_{\mathrm{2}} =\frac{\mathrm{AG}}{\mathrm{EG}}=\frac{\sqrt{\mathrm{49}−\mathrm{EG}^{\mathrm{2}} }}{\mathrm{EG}}=\sqrt{\frac{\mathrm{49}}{\mathrm{EG}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\mathrm{From}\:\mathrm{that}\:\mathrm{and}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{tan}\theta=\mathrm{tan}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)=\frac{\mathrm{tan}\theta_{\mathrm{1}} +\mathrm{tan}\theta_{\mathrm{2}} }{\mathrm{1}−\mathrm{tan}\theta_{\mathrm{1}} \mathrm{tan}\theta_{\mathrm{2}} }\: \\ $$$$=\frac{\sqrt{\frac{\mathrm{36}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}}+\sqrt{\frac{\mathrm{49}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}}}{\mathrm{1}−\sqrt{\left(\frac{\mathrm{36}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right)\left(\sqrt{\left.\frac{\mathrm{49}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right)}\right.}} \\ $$$$\:\mathrm{tan}\theta=\frac{\mathrm{x}\left(\sqrt{\mathrm{36}−\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{49}−\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} −\sqrt{\left(\mathrm{36}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{49}−\mathrm{x}^{\mathrm{2}} \right)}}\:,\mathrm{x}=\mathrm{EG} \\ $$$$\boldsymbol{\mathrm{We}}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{out}}\:\boldsymbol{\mathrm{tan}\theta}=−\mathrm{1}\:\Rightarrow\boldsymbol{\theta}=\mathrm{135}° \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *