Question Number 118887 by rexfordattacudjoe last updated on 20/Oct/20
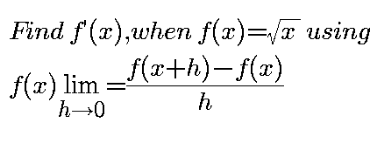
Answered by benjo_mathlover last updated on 20/Oct/20
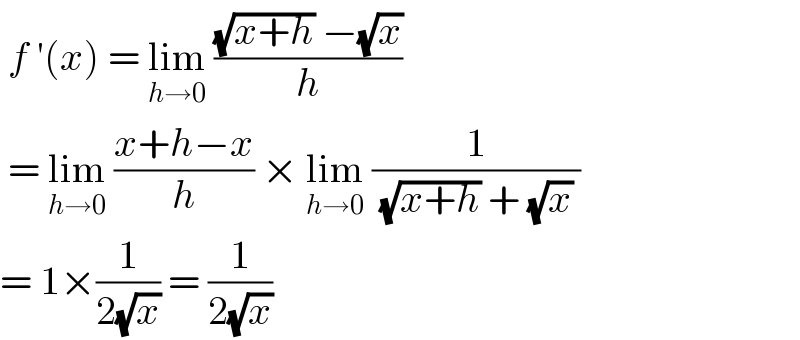
$$\:{f}\:'\left({x}\right)\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}+{h}}\:−\sqrt{{x}}}{{h}} \\ $$$$\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}+{h}−{x}}{{h}}\:×\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{x}+{h}}\:+\:\sqrt{{x}}\:} \\ $$$$=\:\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$
Answered by ebi last updated on 20/Oct/20
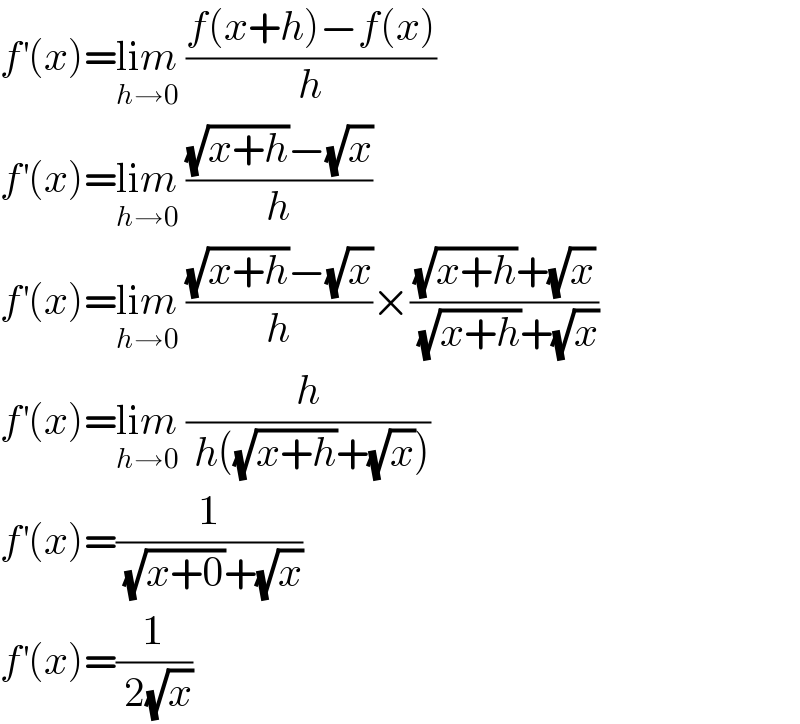
$${f}^{'} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}^{'} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\frac{\sqrt{{x}+{h}}−\sqrt{{x}}}{{h}} \\ $$$${f}^{'} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\frac{\sqrt{{x}+{h}}−\sqrt{{x}}}{{h}}×\frac{\sqrt{{x}+{h}}+\sqrt{{x}}}{\:\sqrt{{x}+{h}}+\sqrt{{x}}} \\ $$$${f}^{'} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\frac{{h}}{\:{h}\left(\sqrt{{x}+{h}}+\sqrt{{x}}\right)} \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{{x}+\mathrm{0}}+\sqrt{{x}}} \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{{x}}} \\ $$
