Question Number 118896 by bobhans last updated on 20/Oct/20

Answered by benjo_mathlover last updated on 20/Oct/20
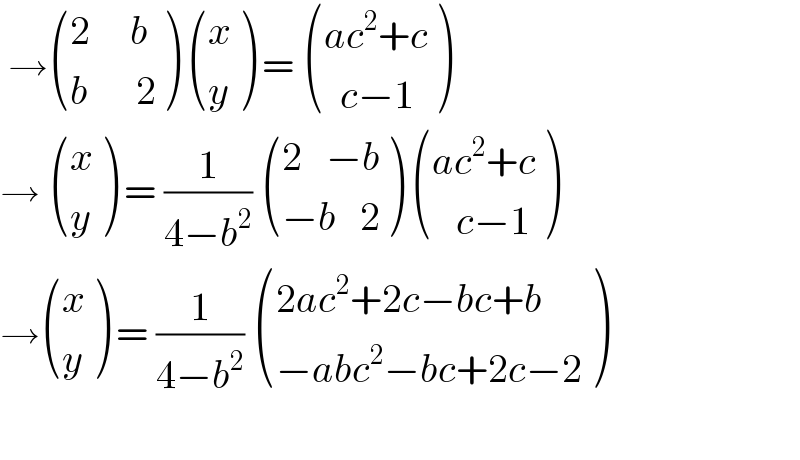
$$\:\rightarrow\begin{pmatrix}{\mathrm{2}\:\:\:\:\:{b}}\\{{b}\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\begin{pmatrix}{{ac}^{\mathrm{2}} +{c}}\\{\:\:{c}−\mathrm{1}}\end{pmatrix} \\ $$$$\rightarrow\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{4}−{b}^{\mathrm{2}} }\:\begin{pmatrix}{\mathrm{2}\:\:\:−{b}}\\{−{b}\:\:\:\mathrm{2}}\end{pmatrix}\:\begin{pmatrix}{{ac}^{\mathrm{2}} +{c}}\\{\:\:\:{c}−\mathrm{1}}\end{pmatrix} \\ $$$$\rightarrow\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{4}−{b}^{\mathrm{2}} }\:\begin{pmatrix}{\mathrm{2}{ac}^{\mathrm{2}} +\mathrm{2}{c}−{bc}+{b}}\\{−{abc}^{\mathrm{2}} −{bc}+\mathrm{2}{c}−\mathrm{2}}\end{pmatrix} \\ $$$$ \\ $$
