Menu Close

Question-118928

Tinku Tara 0 Comments
Pin




Question Number 118928 by mnjuly1970 last updated on 20/Oct/20
Commented by prakash jain last updated on 20/Oct/20
Suggestion: attach image to original question as answer.
$$\mathrm{Suggestion}:\:\:\mathrm{attach}\:\mathrm{image}\:\mathrm{to} \\ $$$$\mathrm{original}\:\mathrm{question}\:\mathrm{as}\:\mathrm{answer}. \\ $$
Commented by mnjuly1970 last updated on 20/Oct/20
thank you for your suggestion..
$$\:\:\:{thank}\:{you}\:{for}\:{your} \\ $$$${suggestion}.. \\ $$
Answered by mathmax by abdo last updated on 11/Feb/21
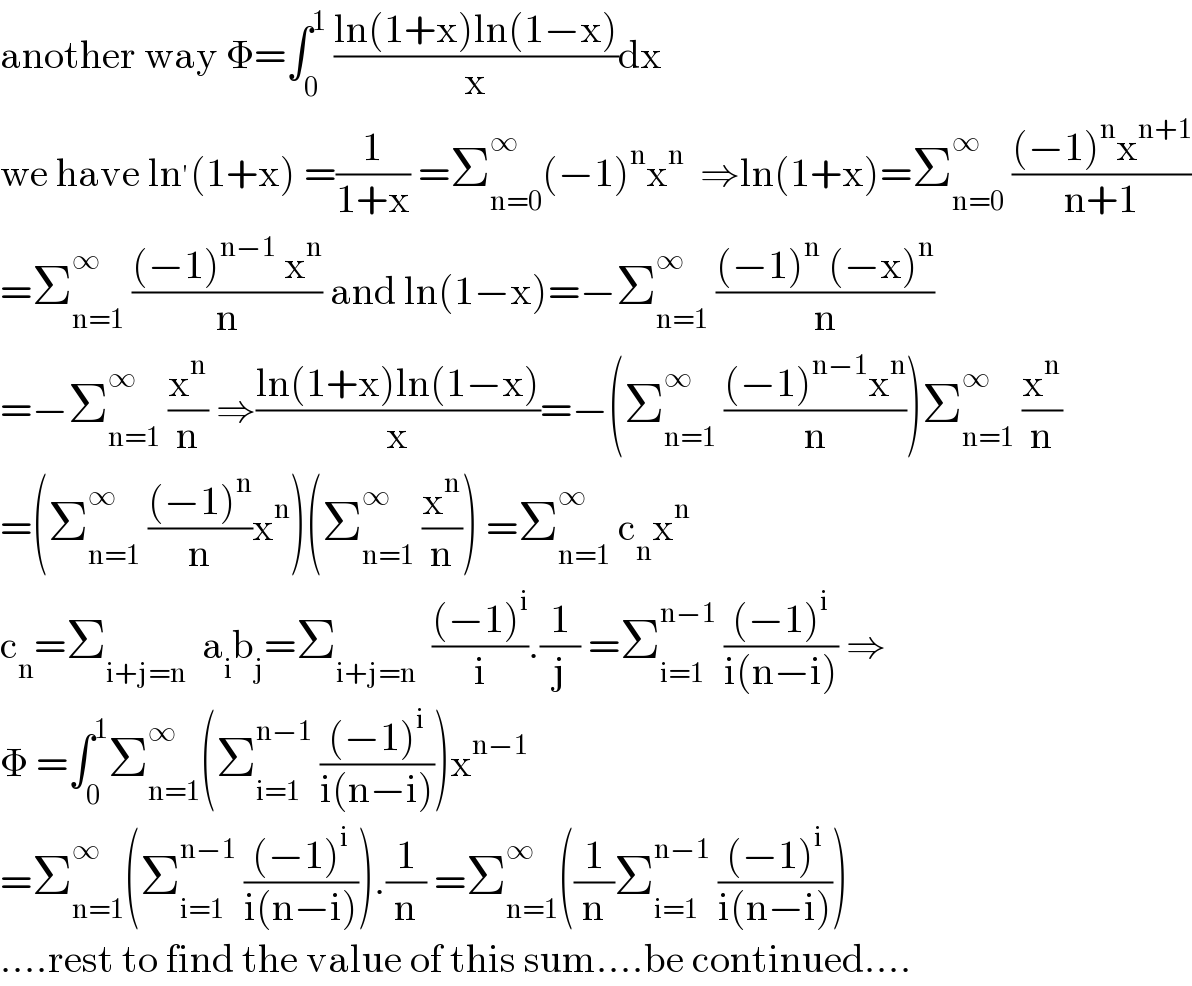
another way Φ=∫_0 ^1 ((ln(1+x)ln(1−x))/x)dx we have ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) and ln(1−x)=−Σ_(n=1) ^∞ (((−1)^n (−x)^n )/n) =−Σ_(n=1) ^∞ (x^n /n) ⇒((ln(1+x)ln(1−x))/x)=−(Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n))Σ_(n=1) ^∞ (x^n /n) =(Σ_(n=1) ^∞ (((−1)^n )/n)x^n )(Σ_(n=1) ^∞ (x^n /n)) =Σ_(n=1) ^∞ c_n x^n c_n =Σ_(i+j=n) a_i b_j =Σ_(i+j=n) (((−1)^i )/i).(1/j) =Σ_(i=1) ^(n−1) (((−1)^i )/(i(n−i))) ⇒ Φ =∫_0 ^1 Σ_(n=1) ^∞ (Σ_(i=1) ^(n−1) (((−1)^i )/(i(n−i))))x^(n−1) =Σ_(n=1) ^∞ (Σ_(i=1) ^(n−1) (((−1)^i )/(i(n−i)))).(1/n) =Σ_(n=1) ^∞ ((1/n)Σ_(i=1) ^(n−1) (((−1)^i )/(i(n−i)))) ....rest to find the value of this sum....be continued....
$$\mathrm{another}\:\mathrm{way}\:\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:\:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\mathrm{and}\:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left(−\mathrm{x}\right)^{\mathrm{n}} }{\mathrm{n}} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}=−\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}} \\ $$$$=\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}} \right)\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{c}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{c}_{\mathrm{n}} =\sum_{\mathrm{i}+\mathrm{j}=\mathrm{n}} \:\:\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{j}} =\sum_{\mathrm{i}+\mathrm{j}=\mathrm{n}} \:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}}.\frac{\mathrm{1}}{\mathrm{j}}\:=\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}\left(\mathrm{n}−\mathrm{i}\right)}\:\Rightarrow \\ $$$$\Phi\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}\left(\mathrm{n}−\mathrm{i}\right)}\right)\mathrm{x}^{\mathrm{n}−\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}\left(\mathrm{n}−\mathrm{i}\right)}\right).\frac{\mathrm{1}}{\mathrm{n}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}\left(\mathrm{n}−\mathrm{i}\right)}\right) \\ $$$$….\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{sum}….\mathrm{be}\:\mathrm{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *