Question-118997

Question Number 118997 by Lordose last updated on 21/Oct/20

Answered by MJS_new last updated on 21/Oct/20

$$\int\frac{{x}^{\mathrm{2}} −\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{5}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{{x}\left(\mathrm{15}{x}^{\mathrm{6}} +\mathrm{110}{x}^{\mathrm{4}} +\mathrm{292}{x}^{\mathrm{2}} +\mathrm{392}\right)}{\mathrm{512}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }−\frac{\mathrm{15}}{\mathrm{512}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}}= \\ $$$$=−\frac{{x}\left(\mathrm{15}{x}^{\mathrm{6}} +\mathrm{110}{x}^{\mathrm{4}} +\mathrm{292}{x}^{\mathrm{2}} +\mathrm{392}\right)}{\mathrm{512}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }−\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{1024}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{x}}{\mathrm{2}}\:+{C} \\ $$

Commented by MJS_new last updated on 21/Oct/20

$$\mathrm{I}\:\mathrm{used}\:\mathrm{and}\:\mathrm{explained}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{method} \\ $$$$\mathrm{several}\:\mathrm{times}\:\mathrm{before},\:\mathrm{search}\:\mathrm{for}\:“\mathrm{Ostrogradski}'' \\ $$$$\mathrm{here}\:\mathrm{on}\:\mathrm{the}\:\mathrm{forum},\:\mathrm{I}\:\mathrm{think}\:\mathrm{you}'\mathrm{ll}\:\mathrm{find}\:\mathrm{enough} \\ $$$$\mathrm{info}\:\mathrm{there} \\ $$

Commented by Ar Brandon last updated on 21/Oct/20

Sir it seems you deleted it before the arrival of "Her Majesty"�� alongside some other posts. Greetings Sir��

Commented by Lordose last updated on 22/Oct/20

Thanks sire. I also used ostrogradski method to resolve the integral.

Commented by Lordose last updated on 22/Oct/20

Nope. It's still in the forum. I thought you speak French ��

Commented by Ar Brandon last updated on 22/Oct/20

Are you referring to me about speaking French, Lordose ?

Commented by Ar Brandon last updated on 22/Oct/20

I do speak French. By-the-way it's the most spoken language in my country��

Commented by MJS_new last updated on 22/Oct/20

I'm from Austria, my native language is German. I have been speaking English for almost 5 decades now. I learned French in school for 4 years but I never used it and forgot most of it. Reading it I'm able to get the meaning somehow...

Commented by Dwaipayan Shikari last updated on 22/Oct/20

Mozart and Beethoven were Austrian and German

Answered by 1549442205PVT last updated on 22/Oct/20

$$\mathrm{I}_{\mathrm{n}} =\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}} }=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{I}_{\mathrm{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int\frac{\mathrm{x}.\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{5}} } \\ $$$$.\mathrm{Put}\:\mathrm{u}=\mathrm{x},\mathrm{dv}=\frac{\mathrm{xdx}}{\left[\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right]^{\mathrm{n}} },\mathrm{du}=\mathrm{dx} \\ $$$$\Rightarrow\mathrm{v}=\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} }\int\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)}{\left[\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right]^{\mathrm{n}} }= \\ $$$$−\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}.\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }.\mathrm{Hence} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{I}_{\mathrm{n}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\left[\frac{\mathrm{x}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }−\right. \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}−\mathrm{1}\right)}\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }\right]\:\mathrm{or} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{I}_{\mathrm{n}−\mathrm{1}} +\frac{\mathrm{x}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{I}}_{\boldsymbol{\mathrm{n}}} =\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\boldsymbol{\mathrm{n}}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }.\frac{\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{3}}{\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{2}}\boldsymbol{\mathrm{I}}_{\boldsymbol{\mathrm{n}}−\mathrm{1}} \\ $$$$\mathrm{Apply}\:\mathrm{on}\:\mathrm{the}\:\mathrm{above}\:\mathrm{problem}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{F}=\int\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{5}} }\mathrm{dx}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }−\mathrm{4}\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{5}} } \\ $$$$\mathrm{F}=\mathrm{I}_{\mathrm{4}} −\mathrm{4I}_{\mathrm{5}} \\ $$$$\mathrm{I}_{\mathrm{5}} =\frac{\mathrm{x}}{\mathrm{4}.\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{7}}{\mathrm{8}}.\mathrm{I}_{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{F}=\mathrm{I}_{\mathrm{4}} −\mathrm{4I}_{\mathrm{5}} =\mathrm{I}_{\mathrm{4}} −\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }−\frac{\mathrm{7}}{\mathrm{8}}\mathrm{I}_{\mathrm{4}} \\ $$$$=−\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{I}_{\mathrm{4}} \\ $$$$\mathrm{I}_{\mathrm{4}} =\frac{\mathrm{x}}{\mathrm{4}.\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{5}}{\mathrm{6}}\left\{\frac{\mathrm{x}}{\mathrm{4}.\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\right. \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{3}}{\mathrm{4}}\left[\frac{\mathrm{x}}{\mathrm{4}.\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right]\right\} \\ $$$$=\frac{\mathrm{x}}{\mathrm{12}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }+\frac{\mathrm{5x}}{\mathrm{192}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{15x}}{\mathrm{3072}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)} \\ $$$$+\frac{\mathrm{15}}{\mathrm{3072}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{F}=\frac{−\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }+\frac{\mathrm{x}}{\mathrm{96}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }+\frac{\mathrm{5x}}{\mathrm{1536}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+ \\ $$$$+\frac{\mathrm{15x}}{\mathrm{24576}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}+\frac{\mathrm{15}}{\:\mathrm{24576}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$

Answered by Bird last updated on 22/Oct/20

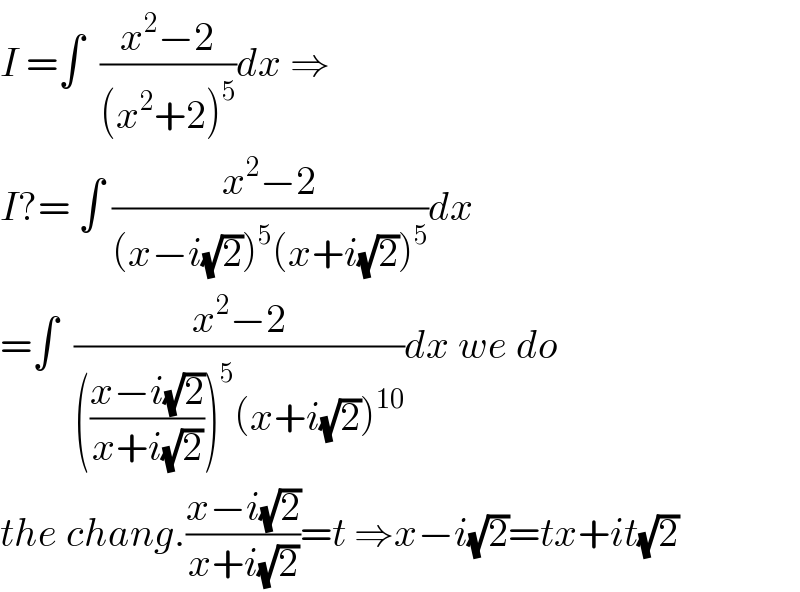
$${I}\:=\int\:\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{5}} }{dx}\:\Rightarrow \\ $$$${I}?=\:\int\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{\left({x}−{i}\sqrt{\mathrm{2}}\right)^{\mathrm{5}} \left({x}+{i}\sqrt{\mathrm{2}}\right)^{\mathrm{5}} }{dx} \\ $$$$=\int\:\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{\left(\frac{{x}−{i}\sqrt{\mathrm{2}}}{{x}+{i}\sqrt{\mathrm{2}}}\right)^{\mathrm{5}} \left({x}+{i}\sqrt{\mathrm{2}}\right)^{\mathrm{10}} }{dx}\:{we}\:{do} \\ $$$${the}\:{chang}.\frac{{x}−{i}\sqrt{\mathrm{2}}}{{x}+{i}\sqrt{\mathrm{2}}}={t}\:\Rightarrow{x}−{i}\sqrt{\mathrm{2}}={tx}+{it}\sqrt{\mathrm{2}} \\ $$

Commented by Bird last updated on 22/Oct/20

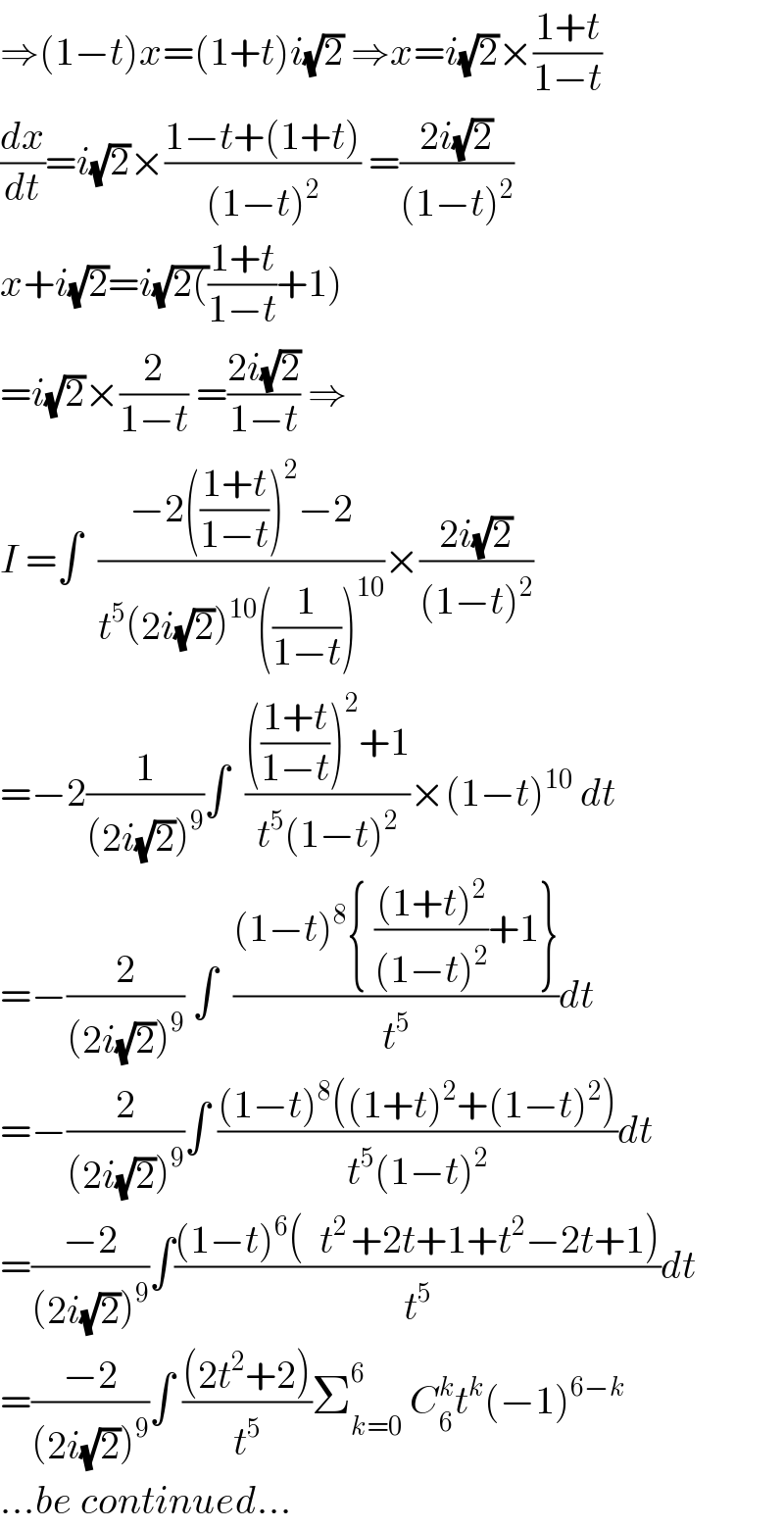
$$\Rightarrow\left(\mathrm{1}−{t}\right){x}=\left(\mathrm{1}+{t}\right){i}\sqrt{\mathrm{2}}\:\Rightarrow{x}={i}\sqrt{\mathrm{2}}×\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}} \\ $$$$\frac{{dx}}{{dt}}={i}\sqrt{\mathrm{2}}×\frac{\mathrm{1}−{t}+\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{i}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} } \\ $$$$\left.{x}+{i}\sqrt{\mathrm{2}}={i}\sqrt{\mathrm{2}\left(\right.}\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}+\mathrm{1}\right) \\ $$$$={i}\sqrt{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{1}−{t}}\:=\frac{\mathrm{2}{i}\sqrt{\mathrm{2}}}{\mathrm{1}−{t}}\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{−\mathrm{2}\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right)^{\mathrm{2}} −\mathrm{2}}{{t}^{\mathrm{5}} \left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{10}} \left(\frac{\mathrm{1}}{\mathrm{1}−{t}}\right)^{\mathrm{10}} }×\frac{\mathrm{2}{i}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\frac{\mathrm{1}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} }\int\:\:\frac{\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right)^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{5}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} }×\left(\mathrm{1}−{t}\right)^{\mathrm{10}} \:{dt} \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} }\:\int\:\:\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{8}} \left\{\:\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }+\mathrm{1}\right\}}{{t}^{\mathrm{5}} }{dt} \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} }\int\:\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{8}} \left(\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +\left(\mathrm{1}−{t}\right)^{\mathrm{2}} \right)}{{t}^{\mathrm{5}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{−\mathrm{2}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} }\int\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{6}} \left(\:\:{t}^{\mathrm{2}\:} +\mathrm{2}{t}+\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)}{{t}^{\mathrm{5}} }{dt} \\ $$$$=\frac{−\mathrm{2}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} }\int\:\frac{\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}\right)}{{t}^{\mathrm{5}} }\sum_{{k}=\mathrm{0}} ^{\mathrm{6}\:} \:{C}_{\mathrm{6}} ^{{k}} {t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{6}−{k}} \\ $$$$…{be}\:{continued}… \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com