Question Number 119013 by zakirullah last updated on 21/Oct/20

Commented by zakirullah last updated on 21/Oct/20

$$\:\:\:\:\:\:\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{component}}\:\boldsymbol{{and}}\: \\ $$$$\:\:\:\:\:\:\boldsymbol{{the}}\:\boldsymbol{{magnitude}}\:\boldsymbol{{of}}\:\boldsymbol{{P}}\overset{\rightarrow} {\boldsymbol{{Q}}} \\ $$$${i}.\:\:\boldsymbol{{P}}\left(−\mathrm{1},\mathrm{2}\right),\:\boldsymbol{{Q}}\left(\mathrm{2},−\mathrm{1}\right) \\ $$$${ii}.\:\:\boldsymbol{{P}}\left(−\mathrm{2},\mathrm{1}\right),\:\boldsymbol{{Q}}\left(\mathrm{2},\mathrm{3}\right) \\ $$$${iii}.\:\:\boldsymbol{{P}}\left(−\mathrm{1},\mathrm{1},\mathrm{2}\right),\:\boldsymbol{{Q}}\left(\mathrm{2},−\mathrm{1},\mathrm{3}\right) \\ $$$${iv}.\:\:\boldsymbol{{P}}\left(\mathrm{2},\mathrm{4},\mathrm{6}\right),\:\:\boldsymbol{{Q}}\left(\mathrm{1},−\mathrm{2},\mathrm{3}\right) \\ $$
Answered by ebi last updated on 21/Oct/20
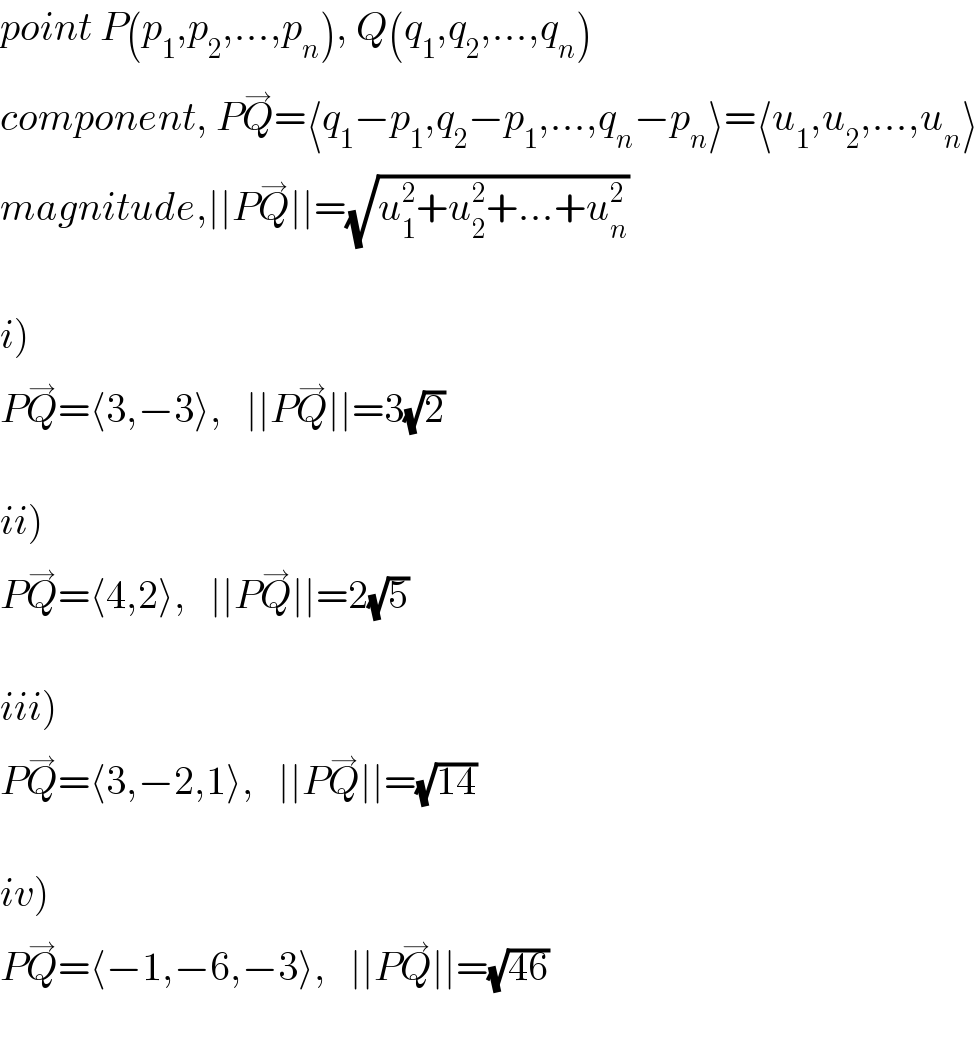
$${point}\:{P}\left({p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,…,{p}_{{n}} \right),\:{Q}\left({q}_{\mathrm{1}} ,{q}_{\mathrm{2}} ,…,{q}_{{n}} \right) \\ $$$${component},\:{P}\overset{\rightarrow} {{Q}}=\langle{q}_{\mathrm{1}} −{p}_{\mathrm{1}} ,{q}_{\mathrm{2}} −{p}_{\mathrm{1}} ,…,{q}_{{n}} −{p}_{{n}} \rangle=\langle{u}_{\mathrm{1}} ,{u}_{\mathrm{2}} ,…,{u}_{{n}} \rangle \\ $$$${magnitude},\mid\mid{P}\overset{\rightarrow} {{Q}}\mid\mid=\sqrt{{u}_{\mathrm{1}} ^{\mathrm{2}} +{u}_{\mathrm{2}} ^{\mathrm{2}} +…+{u}_{{n}} ^{\mathrm{2}} } \\ $$$$ \\ $$$$\left.{i}\right) \\ $$$${P}\overset{\rightarrow} {{Q}}=\langle\mathrm{3},−\mathrm{3}\rangle,\:\:\:\mid\mid{P}\overset{\rightarrow} {{Q}}\mid\mid=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\left.{ii}\right) \\ $$$${P}\overset{\rightarrow} {{Q}}=\langle\mathrm{4},\mathrm{2}\rangle,\:\:\:\mid\mid{P}\overset{\rightarrow} {{Q}}\mid\mid=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$ \\ $$$$\left.{iii}\right) \\ $$$${P}\overset{\rightarrow} {{Q}}=\langle\mathrm{3},−\mathrm{2},\mathrm{1}\rangle,\:\:\:\mid\mid{P}\overset{\rightarrow} {{Q}}\mid\mid=\sqrt{\mathrm{14}} \\ $$$$ \\ $$$$\left.{iv}\right) \\ $$$${P}\overset{\rightarrow} {{Q}}=\langle−\mathrm{1},−\mathrm{6},−\mathrm{3}\rangle,\:\:\:\mid\mid{P}\overset{\rightarrow} {{Q}}\mid\mid=\sqrt{\mathrm{46}} \\ $$$$ \\ $$
Commented by zakirullah last updated on 21/Oct/20

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
