Question Number 119021 by A8;15: last updated on 21/Oct/20
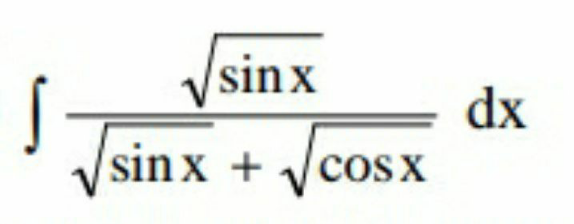
Answered by MJS_new last updated on 21/Oct/20
![∫((√(sin x))/( (√(sin x))+(√(cos x))))dx=∫((√(tan x))/(1+(√(tan x))))dx= [t=(√(tan x)) → dx=((2t)/(t^4 +1))dt] =2∫(t^2 /((t+1)(t^4 +1)))dt now decompose I get ln (t+1) −((1−(√2))/4)ln (t^2 −(√2)t+1) −((1+(√2))/4)ln (t^2 +(√2)t+1) + +(1/2)(arctan ((√2)t−1) −arctan ((√2)t+1)) +C](https://www.tinkutara.com/question/Q119023.png)
$$\int\frac{\sqrt{\mathrm{sin}\:{x}}}{\:\sqrt{\mathrm{sin}\:{x}}+\sqrt{\mathrm{cos}\:{x}}}{dx}=\int\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right)}{dt} \\ $$$$\mathrm{now}\:\mathrm{decompose} \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$$\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\:−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\:+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)\:−\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\right)\:+{C} \\ $$
