Question Number 119032 by Algoritm last updated on 21/Oct/20
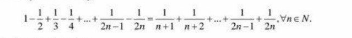
Answered by 1549442205PVT last updated on 22/Oct/20

$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…−\frac{\mathrm{1}}{\mathrm{2n}}=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$\mathrm{Put}\:\mathrm{S}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…−\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$\Rightarrow\:\mathrm{S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2n}}\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\:\frac{\mathrm{1}}{\mathrm{n}}\right)=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$
