Menu Close

Question-119136

Tinku Tara 0 Comments
Pin




Question Number 119136 by Hassen_Timol last updated on 22/Oct/20
Commented by MJS_new last updated on 22/Oct/20
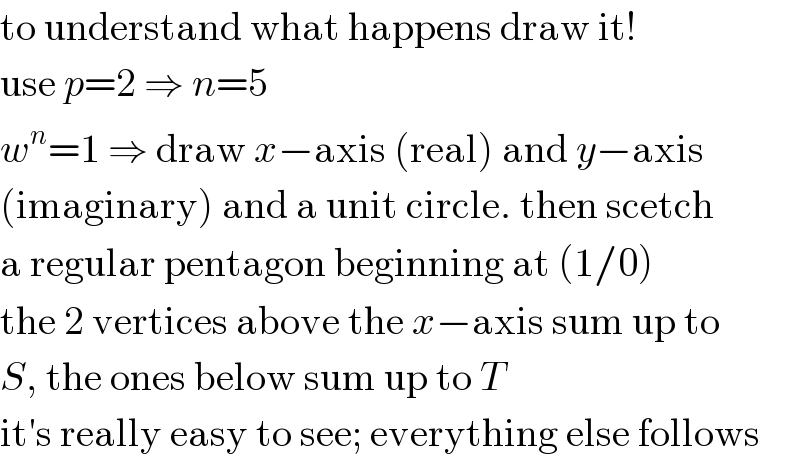
to understand what happens draw it! use p=2 ⇒ n=5 w^n =1 ⇒ draw x−axis (real) and y−axis (imaginary) and a unit circle. then scetch a regular pentagon beginning at (1/0) the 2 vertices above the x−axis sum up to S, the ones below sum up to T it′s really easy to see; everything else follows
$$\mathrm{to}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{happens}\:\mathrm{draw}\:\mathrm{it}! \\ $$$$\mathrm{use}\:{p}=\mathrm{2}\:\Rightarrow\:{n}=\mathrm{5} \\ $$$${w}^{{n}} =\mathrm{1}\:\Rightarrow\:\mathrm{draw}\:{x}−\mathrm{axis}\:\left(\mathrm{real}\right)\:\mathrm{and}\:{y}−\mathrm{axis} \\ $$$$\left(\mathrm{imaginary}\right)\:\mathrm{and}\:\mathrm{a}\:\mathrm{unit}\:\mathrm{circle}.\:\mathrm{then}\:\mathrm{scetch} \\ $$$$\mathrm{a}\:\mathrm{regular}\:\mathrm{pentagon}\:\mathrm{beginning}\:\mathrm{at}\:\left(\mathrm{1}/\mathrm{0}\right) \\ $$$$\mathrm{the}\:\mathrm{2}\:\mathrm{vertices}\:\mathrm{above}\:\mathrm{the}\:{x}−\mathrm{axis}\:\mathrm{sum}\:\mathrm{up}\:\mathrm{to} \\ $$$${S},\:\mathrm{the}\:\mathrm{ones}\:\mathrm{below}\:\mathrm{sum}\:\mathrm{up}\:\mathrm{to}\:{T} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{really}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see};\:\mathrm{everything}\:\mathrm{else}\:\mathrm{follows} \\ $$
Commented by Hassen_Timol last updated on 22/Oct/20
Okay thank you very much
Answered by mathmax by abdo last updated on 22/Oct/20
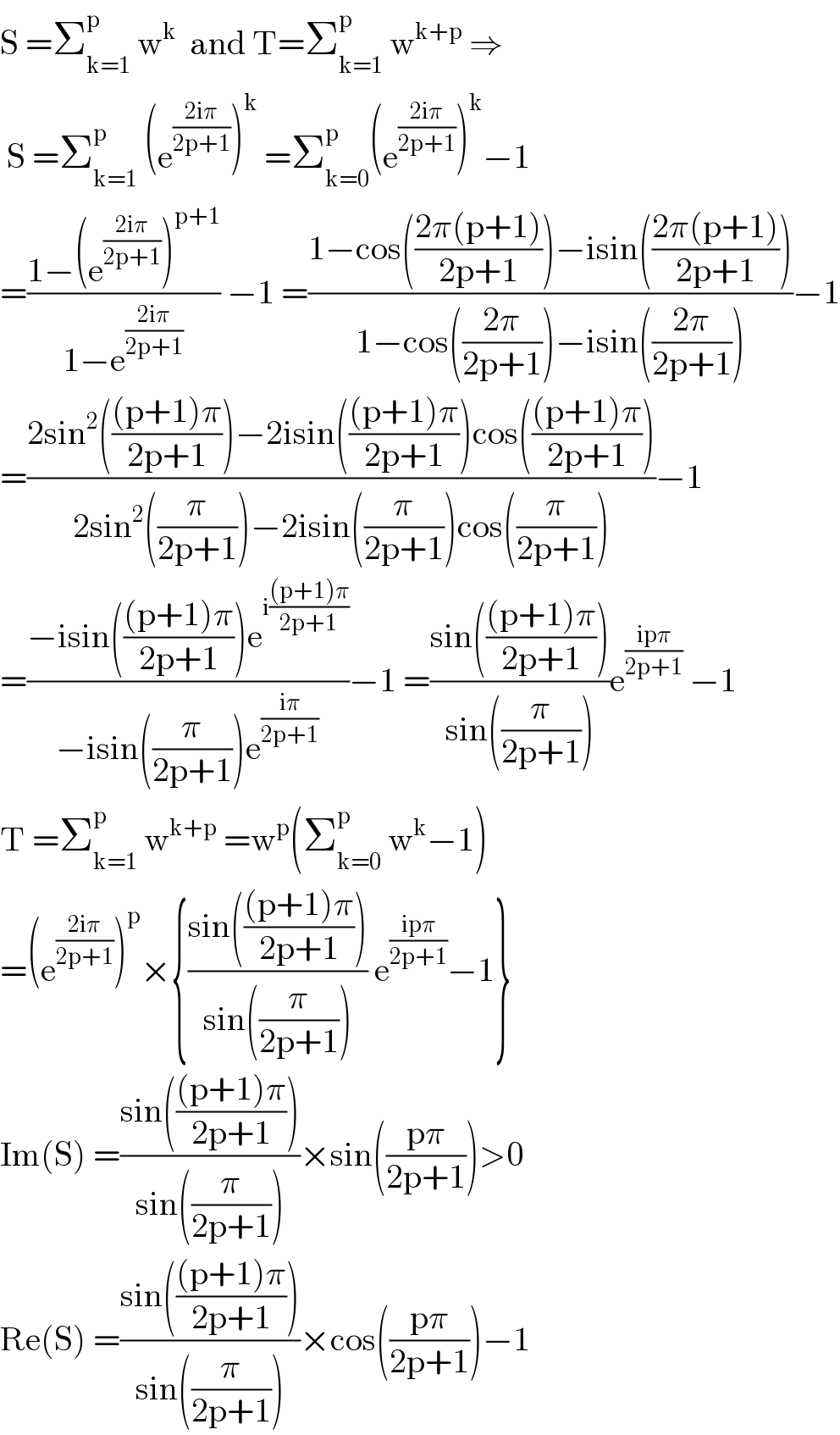
S =Σ_(k=1) ^p w^k and T=Σ_(k=1) ^p w^(k+p) ⇒ S =Σ_(k=1) ^p (e^((2iπ)/(2p+1)) )^k =Σ_(k=0) ^p (e^((2iπ)/(2p+1)) )^k −1 =((1−(e^((2iπ)/(2p+1)) )^(p+1) )/(1−e^((2iπ)/(2p+1)) )) −1 =((1−cos(((2π(p+1))/(2p+1)))−isin(((2π(p+1))/(2p+1))))/(1−cos(((2π)/(2p+1)))−isin(((2π)/(2p+1)))))−1 =((2sin^2 ((((p+1)π)/(2p+1)))−2isin((((p+1)π)/(2p+1)))cos((((p+1)π)/(2p+1))))/(2sin^2 ((π/(2p+1)))−2isin((π/(2p+1)))cos((π/(2p+1)))))−1 =((−isin((((p+1)π)/(2p+1)))e^(i(((p+1)π)/(2p+1))) )/(−isin((π/(2p+1)))e^((iπ)/(2p+1)) ))−1 =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))e^((ipπ)/(2p+1)) −1 T =Σ_(k=1) ^p w^(k+p) =w^p (Σ_(k=0) ^p w^k −1) =(e^((2iπ)/(2p+1)) )^p ×{((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1))))) e^((ipπ)/(2p+1)) −1} Im(S) =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))×sin(((pπ)/(2p+1)))>0 Re(S) =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))×cos(((pπ)/(2p+1)))−1
$$\mathrm{S}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{p}} \:\mathrm{w}^{\mathrm{k}} \:\:\mathrm{and}\:\mathrm{T}=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{p}} \:\mathrm{w}^{\mathrm{k}+\mathrm{p}} \:\Rightarrow \\ $$$$\:\mathrm{S}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{p}} \:\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2p}+\mathrm{1}}} \right)^{\mathrm{k}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{p}} \left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2p}+\mathrm{1}}} \right)^{\mathrm{k}} −\mathrm{1} \\ $$$$=\frac{\mathrm{1}−\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2p}+\mathrm{1}}} \right)^{\mathrm{p}+\mathrm{1}} }{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2p}+\mathrm{1}}} }\:−\mathrm{1}\:=\frac{\mathrm{1}−\mathrm{cos}\left(\frac{\mathrm{2}\pi\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2p}+\mathrm{1}}\right)−\mathrm{isin}\left(\frac{\mathrm{2}\pi\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{1}−\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2p}+\mathrm{1}}\right)−\mathrm{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{2p}+\mathrm{1}}\right)}−\mathrm{1} \\ $$$$=\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)−\mathrm{2isin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)\mathrm{cos}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)−\mathrm{2isin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)}−\mathrm{1} \\ $$$$=\frac{−\mathrm{isin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}} }{−\mathrm{isin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2p}+\mathrm{1}}} }−\mathrm{1}\:=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)}\mathrm{e}^{\frac{\mathrm{ip}\pi}{\mathrm{2p}+\mathrm{1}}} \:−\mathrm{1} \\ $$$$\mathrm{T}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{p}} \:\mathrm{w}^{\mathrm{k}+\mathrm{p}} \:=\mathrm{w}^{\mathrm{p}} \left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{p}} \:\mathrm{w}^{\mathrm{k}} −\mathrm{1}\right) \\ $$$$=\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2p}+\mathrm{1}}} \right)^{\mathrm{p}} ×\left\{\frac{\mathrm{sin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)}\:\mathrm{e}^{\frac{\mathrm{ip}\pi}{\mathrm{2p}+\mathrm{1}}} −\mathrm{1}\right\} \\ $$$$\mathrm{Im}\left(\mathrm{S}\right)\:=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)}×\mathrm{sin}\left(\frac{\mathrm{p}\pi}{\mathrm{2p}+\mathrm{1}}\right)>\mathrm{0} \\ $$$$\mathrm{Re}\left(\mathrm{S}\right)\:=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{p}+\mathrm{1}\right)\pi}{\mathrm{2p}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2p}+\mathrm{1}}\right)}×\mathrm{cos}\left(\frac{\mathrm{p}\pi}{\mathrm{2p}+\mathrm{1}}\right)−\mathrm{1} \\ $$
Commented by Hassen_Timol last updated on 26/Oct/20
Thank you so much you save my entire life

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *