Question Number 119141 by Engr_Jidda last updated on 22/Oct/20

Answered by TANMAY PANACEA last updated on 23/Oct/20

$$\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }+\frac{{dy}}{{dt}}=−{sint} \\ $$$$\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }+\mathrm{4}\frac{{dx}}{{dt}}+\mathrm{3}{x}−{sint}=−{sint} \\ $$$${x}={e}^{{mt}} \\ $$$$\left({m}^{\mathrm{2}} +\mathrm{4}{m}+\mathrm{3}\right){e}^{{mt}} =\mathrm{0} \\ $$$${e}^{{mt}} \neq\mathrm{0} \\ $$$$\left({m}+\mathrm{1}\right)\left({m}+\mathrm{3}\right)=\mathrm{0}\rightarrow{m}=−\mathrm{1},−\mathrm{3} \\ $$$${x}={Ae}^{−{t}} +{Be}^{−\mathrm{3}{t}} \\ $$$${y}={cost}−\frac{{dx}}{{dt}} \\ $$$${y}={cost}+{Ae}^{−{t}} +\mathrm{3}{Be}^{−\mathrm{3}{t}} \\ $$
Commented by Engr_Jidda last updated on 22/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA last updated on 22/Oct/20

$${most}\:{welcome} \\ $$
Commented by Engr_Jidda last updated on 22/Oct/20
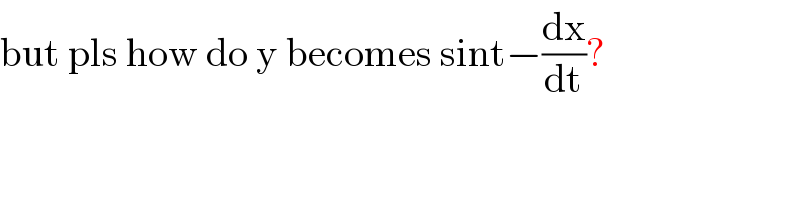
$$\mathrm{but}\:\mathrm{pls}\:\mathrm{how}\:\mathrm{do}\:\mathrm{y}\:\mathrm{becomes}\:\mathrm{sint}−\frac{\mathrm{dx}}{\mathrm{dt}}? \\ $$
Commented by TANMAY PANACEA last updated on 23/Oct/20

$${sorry}\:..{Typo}…{it}\:{should}\:{be}\:{y}={cost}−\frac{{dx}}{{dt}} \\ $$
