Question Number 119158 by mathdave last updated on 22/Oct/20
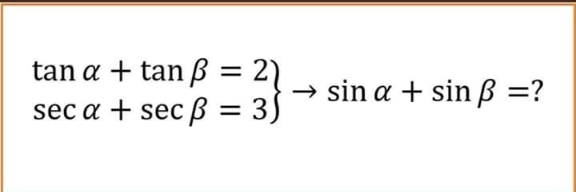
Answered by MJS_new last updated on 22/Oct/20
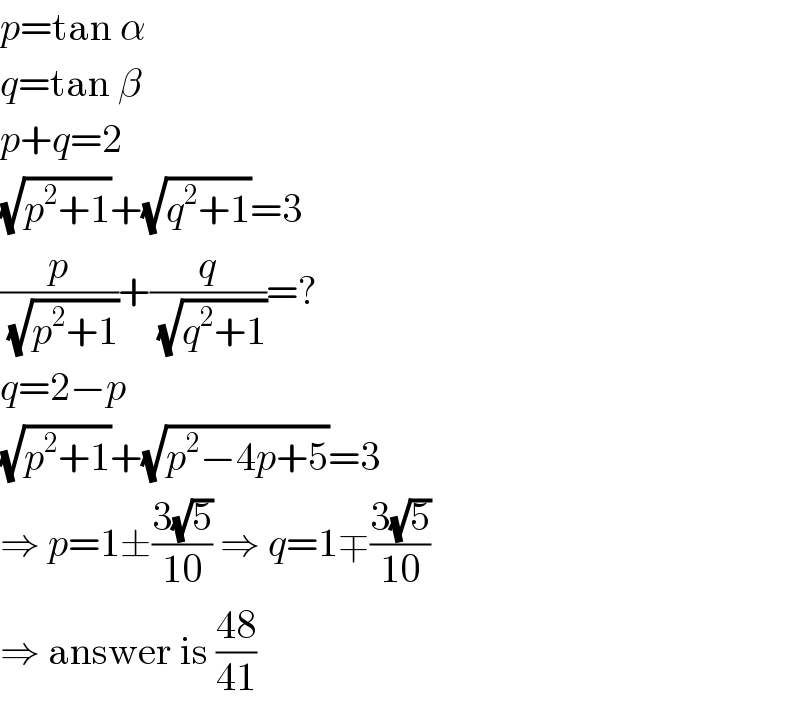
$${p}=\mathrm{tan}\:\alpha \\ $$$${q}=\mathrm{tan}\:\beta \\ $$$${p}+{q}=\mathrm{2} \\ $$$$\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}+\sqrt{{q}^{\mathrm{2}} +\mathrm{1}}=\mathrm{3} \\ $$$$\frac{{p}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}+\frac{{q}}{\:\sqrt{{q}^{\mathrm{2}} +\mathrm{1}}}=? \\ $$$${q}=\mathrm{2}−{p} \\ $$$$\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}+\sqrt{{p}^{\mathrm{2}} −\mathrm{4}{p}+\mathrm{5}}=\mathrm{3} \\ $$$$\Rightarrow\:{p}=\mathrm{1}\pm\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}\:\Rightarrow\:{q}=\mathrm{1}\mp\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{48}}{\mathrm{41}} \\ $$
