Question Number 119173 by help last updated on 22/Oct/20
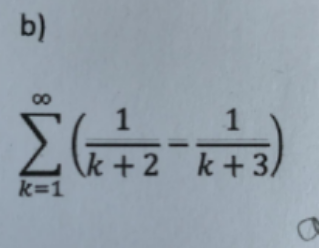
Answered by Olaf last updated on 22/Oct/20
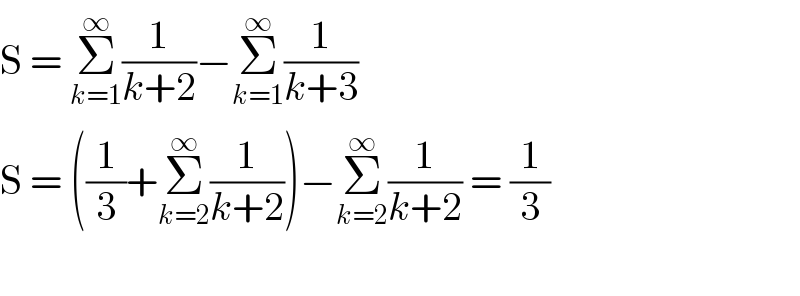
$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{2}}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{3}} \\ $$$$\mathrm{S}\:=\:\left(\frac{\mathrm{1}}{\mathrm{3}}+\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{2}}\right)−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by JDamian last updated on 22/Oct/20
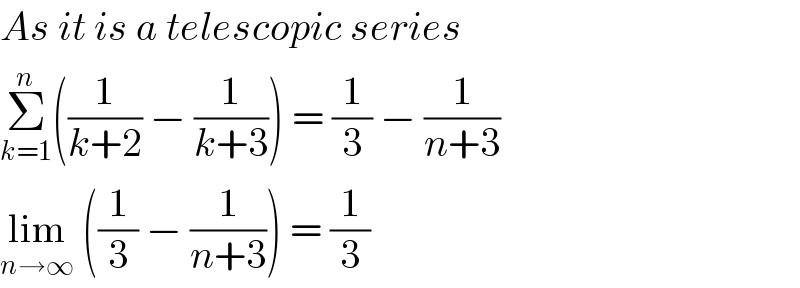
$${As}\:{it}\:{is}\:{a}\:{telescopic}\:{series} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}+\mathrm{2}}\:−\:\frac{\mathrm{1}}{{k}+\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{1}}{{n}+\mathrm{3}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by mathdave last updated on 22/Oct/20
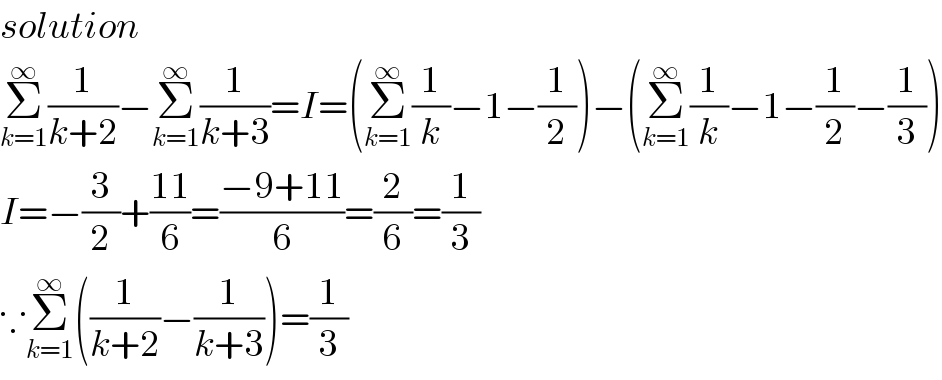
$${solution} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{2}}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{3}}={I}=\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${I}=−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{11}}{\mathrm{6}}=\frac{−\mathrm{9}+\mathrm{11}}{\mathrm{6}}=\frac{\mathrm{2}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\because\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}+\mathrm{2}}−\frac{\mathrm{1}}{{k}+\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
