Question Number 119306 by yahyajan last updated on 23/Oct/20
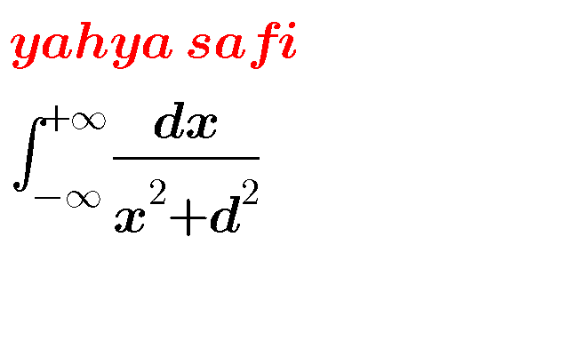
Answered by TANMAY PANACEA last updated on 23/Oct/20
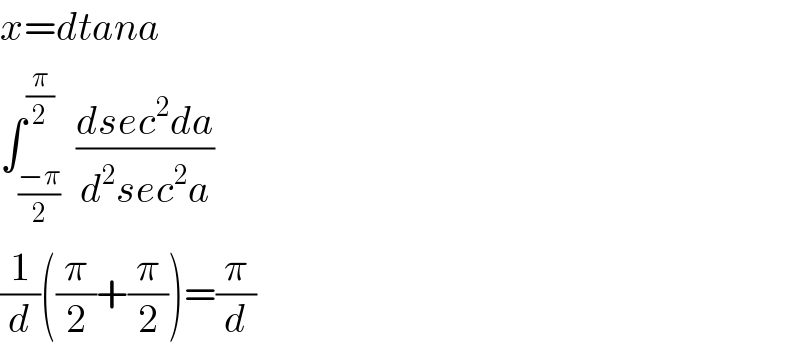
$${x}={dtana} \\ $$$$\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dsec}^{\mathrm{2}} {da}}{{d}^{\mathrm{2}} {sec}^{\mathrm{2}} {a}} \\ $$$$\frac{\mathrm{1}}{{d}}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{{d}} \\ $$
Answered by Olaf last updated on 23/Oct/20
![I = ∫_(−∞) ^(+∞) (dx/(x^2 +d^2 )) = [(1/d)arctan((x/d))]_(−∞) ^(+∞) I = (π/(2d))−(−(π/(2d))) = (π/d)](https://www.tinkutara.com/question/Q119312.png)
$$\mathrm{I}\:=\:\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} +{d}^{\mathrm{2}} }\:=\:\left[\frac{\mathrm{1}}{{d}}\mathrm{arctan}\left(\frac{{x}}{{d}}\right)\right]_{−\infty} ^{+\infty} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}{d}}−\left(−\frac{\pi}{\mathrm{2}{d}}\right)\:=\:\frac{\pi}{{d}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 24/Oct/20
![∫_(−∞) ^(+∞) (dx/(x^2 +d^2 )) =_(x=∣d∣u) ∫_(−∞) ^(+∞) ((∣d∣du)/(d^2 (1+u^2 ))) =(1/(∣d∣))[arctanu]_(−∞) ^(+∞) =(π/(∣d∣)) (if d≠0) if d=0 we get ∫_(−∞) ^(+∞) (dx/x^2 )=[−(1/x)]_(−∞) ^(+∞) =0](https://www.tinkutara.com/question/Q119378.png)
$$\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} }\:=_{\mathrm{x}=\mid\mathrm{d}\mid\mathrm{u}} \:\:\:\int_{−\infty} ^{+\infty} \:\:\frac{\mid\mathrm{d}\mid\mathrm{du}}{\mathrm{d}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mid\mathrm{d}\mid}\left[\mathrm{arctanu}\right]_{−\infty} ^{+\infty} =\frac{\pi}{\mid\mathrm{d}\mid} \\ $$$$\left(\mathrm{if}\:\mathrm{d}\neq\mathrm{0}\right)\:\:\:\:\:\:\mathrm{if}\:\mathrm{d}=\mathrm{0}\:\:\:\mathrm{we}\:\mathrm{get}\:\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }=\left[−\frac{\mathrm{1}}{\mathrm{x}}\right]_{−\infty} ^{+\infty} =\mathrm{0} \\ $$
