Question Number 119315 by zakirullah last updated on 23/Oct/20

Answered by ebi last updated on 23/Oct/20
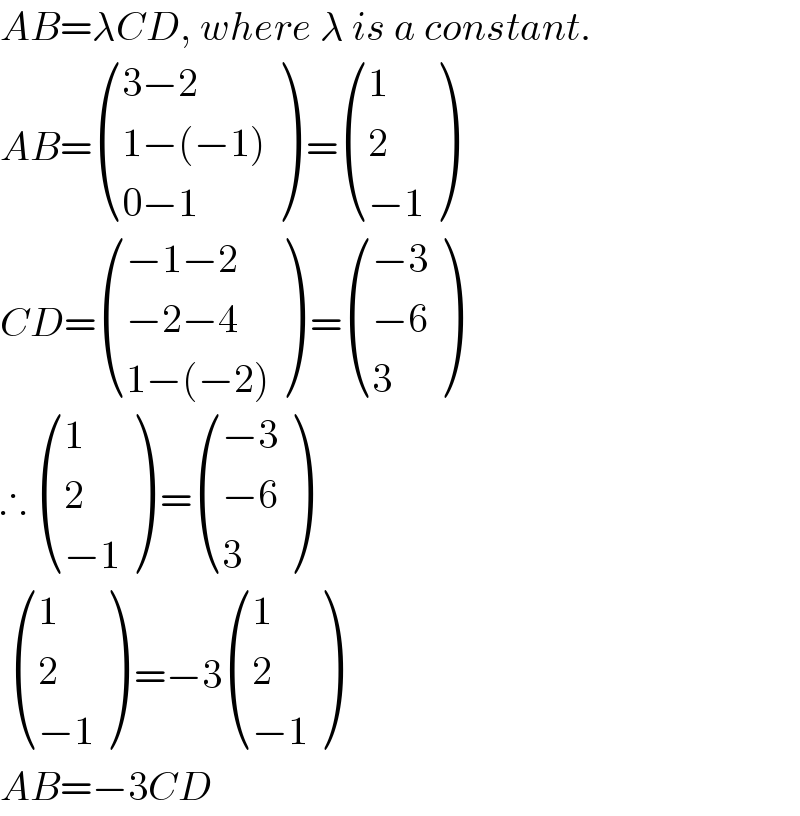
$${AB}=\lambda{CD},\:{where}\:\lambda\:{is}\:{a}\:{constant}. \\ $$$${AB}=\begin{pmatrix}{\mathrm{3}−\mathrm{2}}\\{\mathrm{1}−\left(−\mathrm{1}\right)}\\{\mathrm{0}−\mathrm{1}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$${CD}=\begin{pmatrix}{−\mathrm{1}−\mathrm{2}}\\{−\mathrm{2}−\mathrm{4}}\\{\mathrm{1}−\left(−\mathrm{2}\right)}\end{pmatrix}\:=\begin{pmatrix}{−\mathrm{3}}\\{−\mathrm{6}}\\{\mathrm{3}}\end{pmatrix} \\ $$$$\therefore\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\\{−\mathrm{1}}\end{pmatrix}\:=\begin{pmatrix}{−\mathrm{3}}\\{−\mathrm{6}}\\{\mathrm{3}}\end{pmatrix} \\ $$$$\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\\{−\mathrm{1}}\end{pmatrix}\:=−\mathrm{3}\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$${AB}=−\mathrm{3}{CD} \\ $$
Commented by zakirullah last updated on 23/Oct/20

$$\boldsymbol{{very}}\:\boldsymbol{{great}}\:\boldsymbol{{full}}\:\boldsymbol{{work}} \\ $$
Answered by 1549442205PVT last updated on 24/Oct/20

$$\mathrm{We}\:\mathrm{have}\:\mathrm{A}\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right),\mathrm{B}\left(\mathrm{3},\mathrm{1},\mathrm{0}\right),\mathrm{C}\left(\mathrm{2},\mathrm{4},−\mathrm{2}\right) \\ $$$$\mathrm{and}\:\mathrm{D}\left(−\mathrm{1},−\mathrm{2},\mathrm{1}\right) \\ $$$$\Rightarrow\overset{\rightarrow} {\mathrm{AB}}=\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right),\overset{\rightarrow} {\mathrm{CD}}=\left(−\mathrm{3},−\mathrm{6},\mathrm{3}\right) \\ $$$$\Rightarrow\overset{\rightarrow} {\mathrm{CD}}=\left(−\mathrm{3}\right)\overset{\rightarrow} {\mathrm{AB}}\Rightarrow\overset{\rightarrow} {\mathrm{AB}}//\overset{\rightarrow} {\mathrm{CD}}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
