Question Number 119356 by Lordose last updated on 23/Oct/20

Commented by Dwaipayan Shikari last updated on 23/Oct/20

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}{log}\left(\frac{{x}^{{x}} }{{x}!}\right) \\ $$$$=\frac{\mathrm{1}}{{x}}.{log}\left(\frac{{x}^{{x}} {e}^{{x}} }{{x}^{{x}} .\sqrt{\mathrm{2}\pi{x}}}\right)\left({Stirling}'{s}\:{approximation}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}!=\left(\frac{{n}}{{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}\right. \\ $$$$=\frac{\mathrm{1}}{{x}}{log}\left({e}^{{x}} \right)−\frac{\mathrm{1}}{{x}}{log}\left(\sqrt{\mathrm{2}\pi{x}}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}{log}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}{x}}{log}\left(\mathrm{2}\pi\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{{logx}}{{x}}\:\:\:\:\:\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{logx}}{{x}}=−\frac{{log}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}}=−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+…=\mathrm{0}\right) \\ $$$$=\mathrm{1} \\ $$
Commented by Lordose last updated on 23/Oct/20

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 23/Oct/20
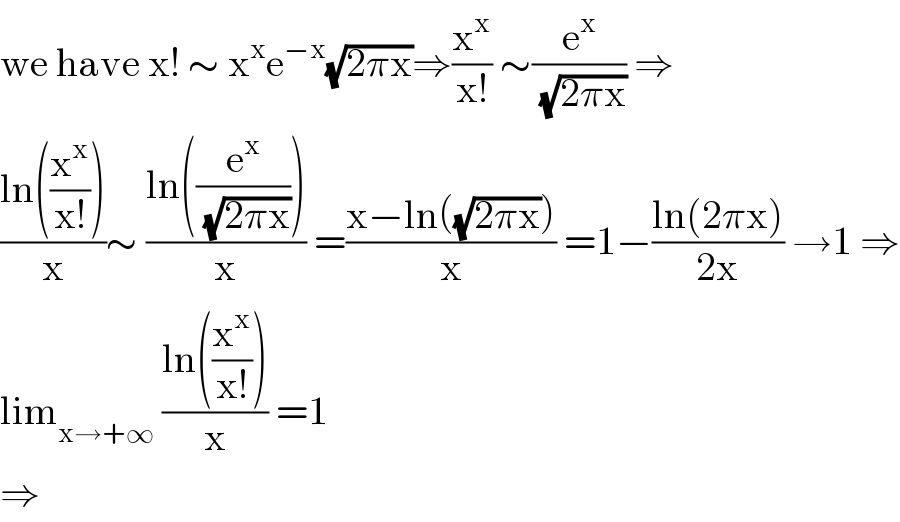
$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}!\:\sim\:\mathrm{x}^{\mathrm{x}} \mathrm{e}^{−\mathrm{x}} \sqrt{\mathrm{2}\pi\mathrm{x}}\Rightarrow\frac{\mathrm{x}^{\mathrm{x}} }{\mathrm{x}!}\:\sim\frac{\mathrm{e}^{\mathrm{x}} }{\:\sqrt{\mathrm{2}\pi\mathrm{x}}}\:\Rightarrow \\ $$$$\frac{\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{x}} }{\mathrm{x}!}\right)}{\mathrm{x}}\sim\:\frac{\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\:\sqrt{\mathrm{2}\pi\mathrm{x}}}\right)}{\mathrm{x}}\:=\frac{\mathrm{x}−\mathrm{ln}\left(\sqrt{\mathrm{2}\pi\mathrm{x}}\right)}{\mathrm{x}}\:=\mathrm{1}−\frac{\mathrm{ln}\left(\mathrm{2}\pi\mathrm{x}\right)}{\mathrm{2x}}\:\rightarrow\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\frac{\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{x}} }{\mathrm{x}!}\right)}{\mathrm{x}}\:=\mathrm{1} \\ $$$$\Rightarrow \\ $$
