Question-119529

Question Number 119529 by I want to learn more last updated on 25/Oct/20

Commented by help last updated on 25/Oct/20

Area of shaded portion {(4/7)×10^2 }=400/7cm^2

$${Area}\:{of}\:{shaded}\:{portion} \\ $$$$\left\{\frac{\mathrm{4}}{\mathrm{7}}×\mathrm{10}^{\mathrm{2}} \right\}=\mathrm{400}/\mathrm{7}{cm}^{\mathrm{2}} \\ $$$$ \\ $$

Commented by benjo_mathlover last updated on 25/Oct/20

((1600)/7) = 228.571429 228.571429 impossible

$$\frac{\mathrm{1600}}{\mathrm{7}}\:=\:\mathrm{228}.\mathrm{571429} \\ $$$$\mathrm{228}.\mathrm{571429} \\ $$$${impossible} \\ $$

Commented by help last updated on 25/Oct/20

this is a shortcut approach. i can prove area of one leaf to be 4/7x^2 if needed

$${this}\:{is}\:{a}\:{shortcut}\:{approach}.\:{i}\:{can}\:{prove}\:{area}\:{of}\:{one}\:{leaf}\:{to}\:{be}\:\mathrm{4}/\mathrm{7}{x}^{\mathrm{2}} \:{if}\:{needed} \\ $$

Commented by benjo_mathlover last updated on 25/Oct/20

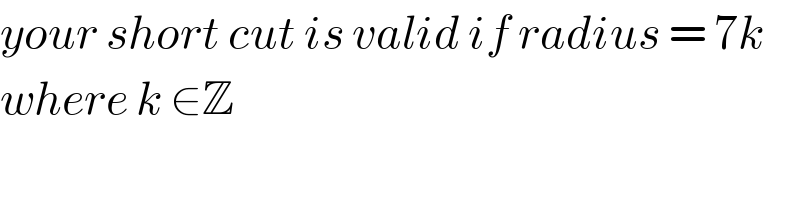
your short cut is valid if radius = 7k where k ∈Z

$${your}\:{short}\:{cut}\:{is}\:{valid}\:{if}\:{radius}\:=\:\mathrm{7}{k}\: \\ $$$${where}\:{k}\:\in\mathbb{Z} \\ $$

Commented by help last updated on 25/Oct/20

400/7 is 100% correct....there^ was a typo before which was corrected...still learning the app usage tho

$$\mathrm{400}/\mathrm{7}\:{is}\:\mathrm{100\%}\:{correct}….{there}^{\:} \:{was}\:{a}\:{typo}\:{before}\:{which}\:{was}\:{corrected}…{still}\:{learning}\:{the}\:{app}\:{usage}\:{tho} \\ $$

Commented by mr W last updated on 25/Oct/20

$${please}\:{don}'{t}\:{write}\:{all}\:{in}\:{one}\:{single}\: \\ $$$${line}! \\ $$

Commented by talminator2856791 last updated on 27/Oct/20

can this diagram be drawn in the drawing tool? i dont know how to draw it

$$\mathrm{can}\:\mathrm{this}\:\mathrm{diagram}\:\mathrm{be}\:\mathrm{drawn}\:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{drawing}\:\mathrm{tool}?\:\mathrm{i}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{draw}\: \\ $$$$\mathrm{it} \\ $$

Answered by mr W last updated on 25/Oct/20

shaded area=8 sectors= 2 red circles with radius 5 − 2 green squares with side length 5(√2) =2×π×5^2 −2×(5(√2))^2 =50(π−2) =57.08 cm^2

$${shaded}\:{area}=\mathrm{8}\:{sectors}= \\ $$$$\mathrm{2}\:{red}\:{circles}\:{with}\:{radius}\:\mathrm{5}\:− \\ $$$$\mathrm{2}\:{green}\:{squares}\:{with}\:{side}\:{length}\:\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{2}×\pi×\mathrm{5}^{\mathrm{2}} −\mathrm{2}×\left(\mathrm{5}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{50}\left(\pi−\mathrm{2}\right) \\ $$$$=\mathrm{57}.\mathrm{08}\:{cm}^{\mathrm{2}} \\ $$

Commented by mr W last updated on 25/Oct/20

Commented by talminator2856791 last updated on 27/Oct/20

very nice drawing. did you draw it with the drawing tool?

$$\mathrm{very}\:\mathrm{nice}\:\mathrm{drawing}.\:\mathrm{did}\:\mathrm{you}\:\mathrm{draw}\:\mathrm{it}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{drawing}\:\mathrm{tool}? \\ $$

Answered by ebi last updated on 25/Oct/20

lets take the first quarter of ABCD at point A area of sector ( center at midpoint AB,r=5cm) =(1/4)πr^2 =(1/4)(((22)/7))(5^2 )=19.64cm^2 area of triangle (right−angle triangle at midpoint AB) =(1/2)(5)(5)=12.5cm^2 area of half of the shaded region at the first quarter =19.64−12.5=7.14cm^2 area of shaded region at the first quarter =2×7.14=14.28cm^2 thus, total area of shaded region =4×14.28=57.12cm^2

$$ \\ $$$${lets}\:{take}\:{the}\:{first}\:{quarter}\:{of}\:{ABCD} \\ $$$${at}\:{point}\:{A} \\ $$$$ \\ $$$${area}\:{of}\:{sector}\:\left(\:{center}\:{at}\:{midpoint}\right. \\ $$$$\left.{AB},{r}=\mathrm{5}{cm}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\pi{r}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{22}}{\mathrm{7}}\right)\left(\mathrm{5}^{\mathrm{2}} \right)=\mathrm{19}.\mathrm{64}{cm}^{\mathrm{2}} \\ $$$${area}\:{of}\:{triangle}\:\left({right}−{angle}\:{triangle}\right. \\ $$$$\left.{at}\:{midpoint}\:{AB}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}\right)\left(\mathrm{5}\right)=\mathrm{12}.\mathrm{5}{cm}^{\mathrm{2}} \\ $$$${area}\:{of}\:{half}\:{of}\:{the}\:{shaded}\:{region}\:{at} \\ $$$${the}\:{first}\:{quarter} \\ $$$$=\mathrm{19}.\mathrm{64}−\mathrm{12}.\mathrm{5}=\mathrm{7}.\mathrm{14}{cm}^{\mathrm{2}} \\ $$$${area}\:{of}\:{shaded}\:{region}\:{at}\:{the}\:{first} \\ $$$${quarter} \\ $$$$=\mathrm{2}×\mathrm{7}.\mathrm{14}=\mathrm{14}.\mathrm{28}{cm}^{\mathrm{2}} \\ $$$$ \\ $$$${thus}, \\ $$$${total}\:{area}\:{of}\:{shaded}\:{region} \\ $$$$=\mathrm{4}×\mathrm{14}.\mathrm{28}=\mathrm{57}.\mathrm{12}{cm}^{\mathrm{2}} \\ $$$$ \\ $$

Answered by TANMAY PANACEA last updated on 25/Oct/20

area of each leaf=2x area of each triangular curved area y 4(2x)+4y=a^2 again ares of triangle 2x+y=(1/2)×a×(a/2)=(a^2 /4) ∡DOC=(π/2) so radius ofcurve=(a/2) 2(2x)+y=((πa^2 )/2) 4x+y=((πa^2 )/2) ×4 8x+4y=a^2 16+4y=2πa^2 8x+4y=a^2 8x=a^2 (2π−1) area shadded=8x

$${area}\:{of}\:{each}\:{leaf}=\mathrm{2}{x} \\ $$$${area}\:{of}\:{each}\:{triangular}\:{curved}\:{area}\:{y} \\ $$$$\mathrm{4}\left(\mathrm{2}{x}\right)+\mathrm{4}{y}={a}^{\mathrm{2}} \\ $$$${again}\:{ares}\:{of}\:{triangle} \\ $$$$\mathrm{2}{x}+{y}=\frac{\mathrm{1}}{\mathrm{2}}×{a}×\frac{{a}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\measuredangle{DOC}=\frac{\pi}{\mathrm{2}} \\ $$$${so}\:{radius}\:{ofcurve}=\frac{{a}}{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{2}{x}\right)+{y}=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}\:\: \\ $$$$\mathrm{4}{x}+{y}=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}\:×\mathrm{4} \\ $$$$\mathrm{8}{x}+\mathrm{4}{y}={a}^{\mathrm{2}} \\ $$$$\mathrm{16}+\mathrm{4}{y}=\mathrm{2}\pi{a}^{\mathrm{2}} \\ $$$$\mathrm{8}{x}+\mathrm{4}{y}={a}^{\mathrm{2}} \\ $$$$\mathrm{8}{x}={a}^{\mathrm{2}} \left(\mathrm{2}\pi−\mathrm{1}\right) \\ $$$${area}\:{shadded}=\mathrm{8}{x} \\ $$$$ \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

$${Pls}\:{find}\:{error}\:{in}\:{this}\:{calculation}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply