Question Number 119572 by zakirullah last updated on 25/Oct/20
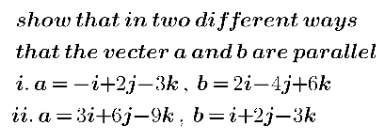
Commented by bemath last updated on 25/Oct/20
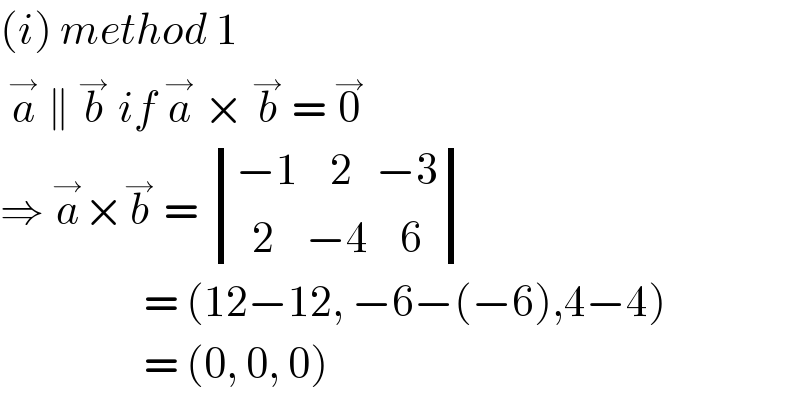
$$\left({i}\right)\:{method}\:\mathrm{1} \\ $$$$\:\overset{\rightarrow} {{a}}\:\parallel\:\overset{\rightarrow} {{b}}\:{if}\:\overset{\rightarrow} {{a}}\:×\:\overset{\rightarrow} {{b}}\:=\:\overset{\rightarrow} {\mathrm{0}} \\ $$$$\Rightarrow\:\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:=\:\begin{vmatrix}{−\mathrm{1}\:\:\:\:\mathrm{2}\:\:\:−\mathrm{3}}\\{\:\:\mathrm{2}\:\:\:\:−\mathrm{4}\:\:\:\:\mathrm{6}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{12}−\mathrm{12},\:−\mathrm{6}−\left(−\mathrm{6}\right),\mathrm{4}−\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{0},\:\mathrm{0},\:\mathrm{0}\right) \\ $$
Commented by bemath last updated on 25/Oct/20
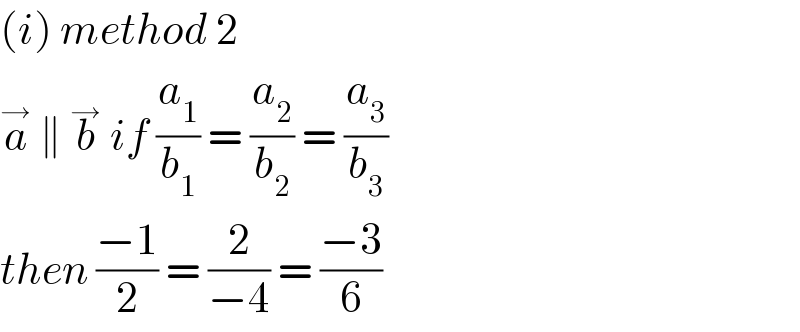
$$\left({i}\right)\:{method}\:\mathrm{2} \\ $$$$\overset{\rightarrow} {{a}}\:\parallel\:\overset{\rightarrow} {{b}}\:{if}\:\frac{{a}_{\mathrm{1}} }{{b}_{\mathrm{1}} }\:=\:\frac{{a}_{\mathrm{2}} }{{b}_{\mathrm{2}} }\:=\:\frac{{a}_{\mathrm{3}} }{{b}_{\mathrm{3}} } \\ $$$${then}\:\frac{−\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{2}}{−\mathrm{4}}\:=\:\frac{−\mathrm{3}}{\mathrm{6}} \\ $$
Commented by zakirullah last updated on 25/Oct/20

$$\boldsymbol{{you}}\:\boldsymbol{{are}}\:\boldsymbol{{the}}\:\boldsymbol{{great}}! \\ $$
