Question Number 119618 by help last updated on 25/Oct/20
Answered by ebi last updated on 25/Oct/20

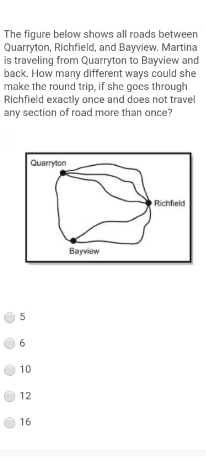
$${Option}\:\mathrm{1} \\ $$$${Quarryton}−{Richfield}−{Bayview}−{Quarryton} \\ $$$${Quarryton}−{Richfield}\rightarrow\mathrm{3}{ways} \\ $$$${Richfield}−{Bayview}\rightarrow\mathrm{2}{ways} \\ $$$${Bayview}−{Quarryton}\rightarrow\mathrm{1}{ways} \\ $$$${Total}\:{of}\:{possible}\:{waysfor}\:{option}\:\mathrm{1}=\mathrm{6}{ways} \\ $$$$ \\ $$$${Option}\:\mathrm{2} \\ $$$${Quarryton}−{Bayview}−{Richfield}−{Quarryton} \\ $$$${Quarryton}−{Bayview}\rightarrow\mathrm{1}{way} \\ $$$${Bayview}−{Richfield}\rightarrow\mathrm{2}{ways} \\ $$$${Richfield}−{Quarryton}\rightarrow\mathrm{3}{ways} \\ $$$${Total}\:{of}\:{possible}\:{ways}\:{option}\:\mathrm{2}=\mathrm{6}{ways} \\ $$$$ \\ $$$${Overall}\:{possible}\:{ways}=\mathrm{12}{ways} \\ $$
