Question Number 119647 by
IE last updated on 26/Oct/20

Answered by Ar Brandon last updated on 26/Oct/20
![En coordonne^� es sphe^� riques nous avons { ((x=rsinϕcosθ),(r∈[0,R])),((y=rsinϕsinθ),(θ∈[0,π])),((z=rcosϕ),(ϕ∈[0,α])) :} ⇒Ω=∫_0 ^π ∫_0 ^α ∫_0 ^R ((∣∣J∣∣)/(rcosϕ))drdϕdθ , ∣∣J∣∣=la matrice Jacobien =∫_0 ^π ∫_0 ^α ∫_0 ^R ((r^2 sinϕ)/(rcosϕ))drdϕdθ=∫_0 ^π ∫_0 ^α ∫_0 ^R rtanϕdrdϕdθ =[(r^2 /2)]_0 ^R [((ln∣secϕ∣)/1)]_0 ^α [(θ/1)]_0 ^π =((πR^2 ln∣secα∣)/2)](https://www.tinkutara.com/question/Q119652.png)
$$\mathrm{En}\:\mathrm{coordonn}\acute {\mathrm{e}es}\:\mathrm{sph}\acute {\mathrm{e}riques}\:\mathrm{nous}\:\mathrm{avons} \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{rsin}\varphi\mathrm{cos}\theta}&{\mathrm{r}\in\left[\mathrm{0},\mathrm{R}\right]}\\{\mathrm{y}=\mathrm{rsin}\varphi\mathrm{sin}\theta}&{\theta\in\left[\mathrm{0},\pi\right]}\\{\mathrm{z}=\mathrm{rcos}\varphi}&{\varphi\in\left[\mathrm{0},\alpha\right]}\end{cases} \\ $$$$\Rightarrow\Omega=\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\alpha} \int_{\mathrm{0}} ^{\mathrm{R}} \frac{\mid\mid\mathrm{J}\mid\mid}{\mathrm{rcos}\varphi}\mathrm{drd}\varphi\mathrm{d}\theta\:,\:\mid\mid\mathrm{J}\mid\mid=\mathrm{la}\:\mathrm{matrice}\:\mathrm{Jacobien} \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\alpha} \int_{\mathrm{0}} ^{\mathrm{R}} \frac{\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi}{\mathrm{rcos}\varphi}\mathrm{drd}\varphi\mathrm{d}\theta=\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\alpha} \int_{\mathrm{0}} ^{\mathrm{R}} \mathrm{rtan}\varphi\mathrm{drd}\varphi\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{R}} \left[\frac{\mathrm{ln}\mid\mathrm{sec}\varphi\mid}{\mathrm{1}}\right]_{\mathrm{0}} ^{\alpha} \left[\frac{\theta}{\mathrm{1}}\right]_{\mathrm{0}} ^{\pi} =\frac{\pi\mathrm{R}^{\mathrm{2}} \mathrm{ln}\mid\mathrm{sec}\alpha\mid}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 26/Oct/20
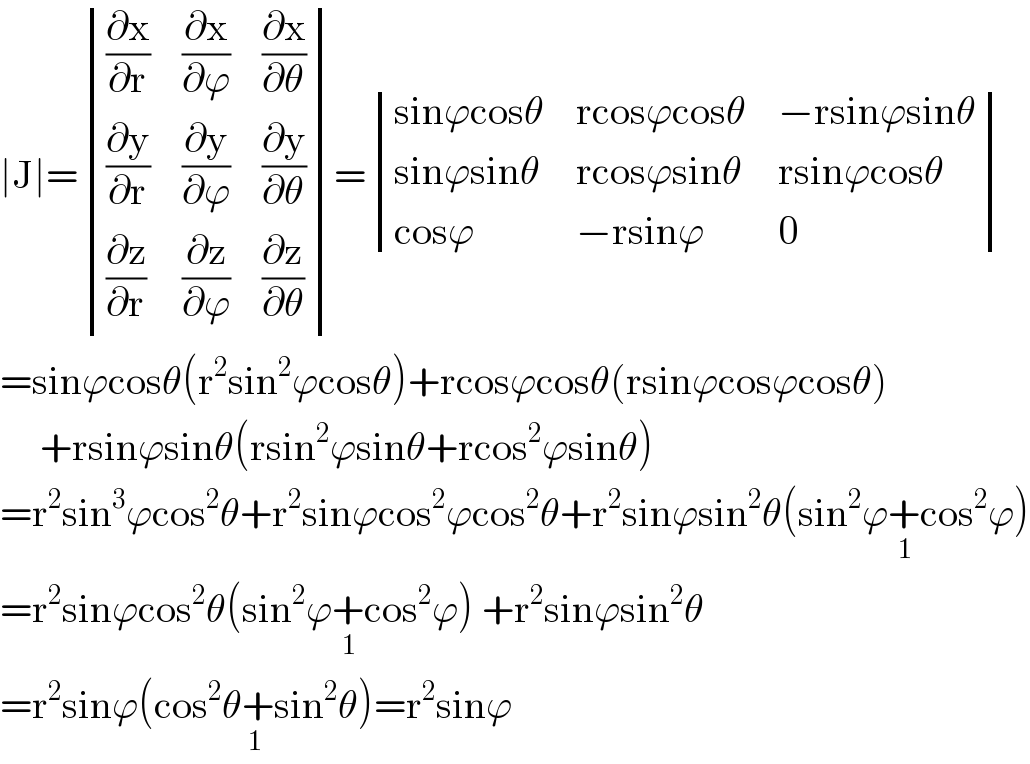
$$\mid\mathrm{J}\mid=\begin{vmatrix}{\frac{\partial\mathrm{x}}{\partial\mathrm{r}}}&{\frac{\partial\mathrm{x}}{\partial\varphi}}&{\frac{\partial\mathrm{x}}{\partial\theta}}\\{\frac{\partial\mathrm{y}}{\partial\mathrm{r}}}&{\frac{\partial\mathrm{y}}{\partial\varphi}}&{\frac{\partial\mathrm{y}}{\partial\theta}}\\{\frac{\partial\mathrm{z}}{\partial\mathrm{r}}}&{\frac{\partial\mathrm{z}}{\partial\varphi}}&{\frac{\partial\mathrm{z}}{\partial\theta}}\end{vmatrix}=\begin{vmatrix}{\mathrm{sin}\varphi\mathrm{cos}\theta}&{\mathrm{rcos}\varphi\mathrm{cos}\theta}&{−\mathrm{rsin}\varphi\mathrm{sin}\theta}\\{\mathrm{sin}\varphi\mathrm{sin}\theta}&{\mathrm{rcos}\varphi\mathrm{sin}\theta}&{\mathrm{rsin}\varphi\mathrm{cos}\theta}\\{\mathrm{cos}\varphi}&{−\mathrm{rsin}\varphi}&{\mathrm{0}}\end{vmatrix} \\ $$$$=\mathrm{sin}\varphi\mathrm{cos}\theta\left(\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \varphi\mathrm{cos}\theta\right)+\mathrm{rcos}\varphi\mathrm{cos}\theta\left(\mathrm{rsin}\varphi\mathrm{cos}\varphi\mathrm{cos}\theta\right) \\ $$$$\:\:\:\:\:+\mathrm{rsin}\varphi\mathrm{sin}\theta\left(\mathrm{rsin}^{\mathrm{2}} \varphi\mathrm{sin}\theta+\mathrm{rcos}^{\mathrm{2}} \varphi\mathrm{sin}\theta\right) \\ $$$$=\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{3}} \varphi\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi\mathrm{cos}^{\mathrm{2}} \varphi\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi\mathrm{sin}^{\mathrm{2}} \theta\underset{\mathrm{1}} {\left(\mathrm{sin}^{\mathrm{2}} \varphi+\mathrm{cos}^{\mathrm{2}} \varphi\right)} \\ $$$$=\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi\mathrm{cos}^{\mathrm{2}} \theta\underset{\mathrm{1}} {\left(\mathrm{sin}^{\mathrm{2}} \varphi+\mathrm{cos}^{\mathrm{2}} \varphi\right)}\:+\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$=\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi\underset{\mathrm{1}} {\left(\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right)}=\mathrm{r}^{\mathrm{2}} \mathrm{sin}\varphi \\ $$
