Question Number 119733 by bemath last updated on 26/Oct/20
Commented by bemath last updated on 26/Oct/20
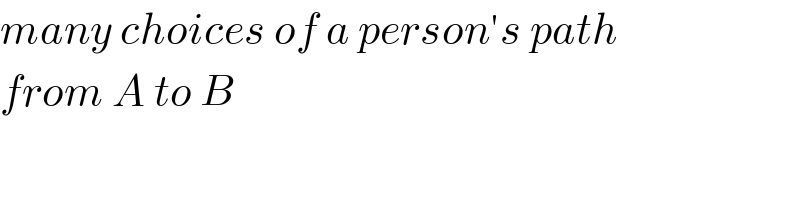
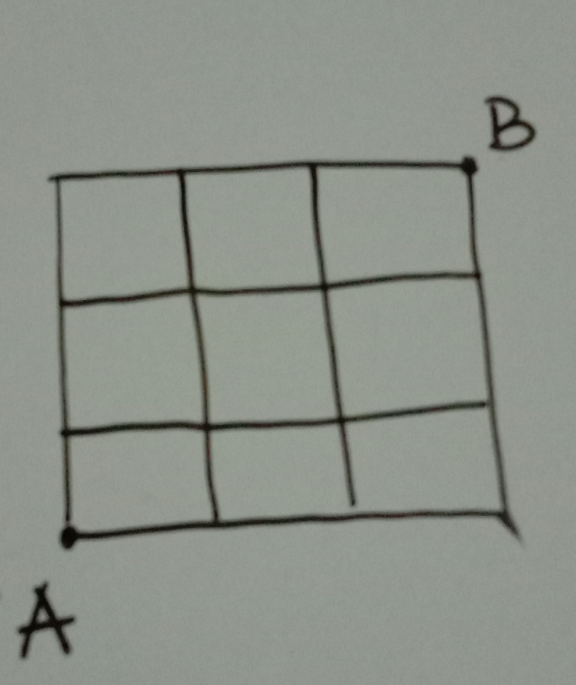
$${many}\:{choices}\:{of}\:{a}\:{person}'{s}\:{path} \\ $$$${from}\:{A}\:{to}\:{B} \\ $$
Commented by MJS_new last updated on 26/Oct/20

$$\mathrm{we}\:\mathrm{need}\:\mathrm{more}\:\mathrm{info}.\:\mathrm{each}\:\mathrm{point}\:\mathrm{allowed} \\ $$$$\mathrm{once}\:\mathrm{or}…? \\ $$$$\mathrm{without}\:\mathrm{restrictions}\:\mathrm{the}\:\mathrm{number}\:\mathrm{is}\:\infty \\ $$$$\left(\mathrm{I}\:\mathrm{could}\:\mathrm{walk}\:\mathrm{around}\:\mathrm{the}\:\mathrm{inner}\:\mathrm{square}\:\mathrm{1},\:\mathrm{2},\:…\right. \\ $$$$\left.\mathrm{times}\right) \\ $$
Commented by soumyasaha last updated on 26/Oct/20

$$ \\ $$$$\:\:\frac{\mathrm{6}!}{\mathrm{3}!.\mathrm{3}!}\:=\:\mathrm{20} \\ $$
Commented by bemath last updated on 26/Oct/20

$${how}\:{got}\:{it}\:{sir}? \\ $$
Commented by bemath last updated on 26/Oct/20
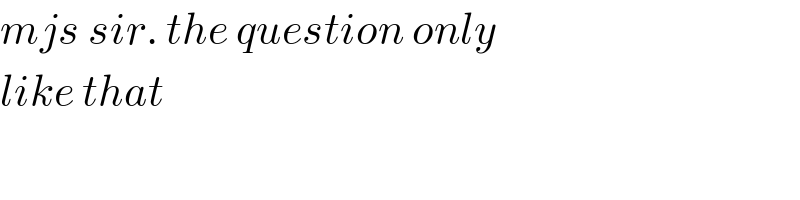
$${mjs}\:{sir}.\:{the}\:{question}\:{only}\: \\ $$$${like}\:{that} \\ $$
Answered by mr W last updated on 26/Oct/20

$${we}\:{have}\:{unique}\:{solution}\:{only}\:{if}\:{it} \\ $$$${is}\:{restricted}\:{that}\:{we}\:{move}\:{upwards}\:{or} \\ $$$${rightwards}\:{only}. \\ $$$${we}\:{have}\:\mathrm{3}\:{upwards}\:{steps}\:{and}\:\mathrm{3} \\ $$$${rightwards}\:{steps}.\:{each}\:{arrangement} \\ $$$${is}\:{a}\:{path}.\:{so}\:{tatally}\:{we}\:{have} \\ $$$$\frac{\mathrm{6}!}{\mathrm{3}!\mathrm{3}!}=\mathrm{20}\:{pathes}. \\ $$
Commented by bemath last updated on 27/Oct/20

Commented by bemath last updated on 27/Oct/20
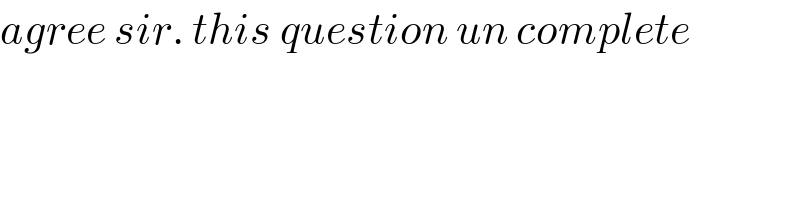
$${agree}\:{sir}.\:{this}\:{question}\:{un}\:{complete} \\ $$
