Question Number 119803 by repentence last updated on 27/Oct/20
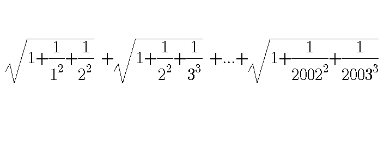
Answered by Dwaipayan Shikari last updated on 27/Oct/20

$${T}_{{n}} =\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$=\sqrt{\frac{\left({n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +{n}^{\mathrm{2}} \right)+{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}+{n}^{\mathrm{2}} }{\left({n}\left({n}+\mathrm{1}\right)\right)^{\mathrm{2}} }} \\ $$$$=\sqrt{\frac{{n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}}{\left({n}\left({n}+\mathrm{1}\right)\right)^{\mathrm{2}} }}\:\:\:\:\:\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)^{\mathrm{2}} ={n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1} \\ $$$$=\frac{\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)}{{n}\left({n}+\mathrm{1}\right)} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2002}} {\sum}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2002}} {\sum}}\mathrm{1}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$=\mathrm{2002}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2003}} \\ $$$$=\mathrm{2003}−\frac{\mathrm{1}}{\mathrm{2003}}=\mathrm{2002}.\mathrm{999500748876684} \\ $$
