Question Number 119866 by Dwaipayan Shikari last updated on 27/Oct/20

Commented by Ar Brandon last updated on 27/Oct/20
Where did you get this, bro ?����
Commented by Dwaipayan Shikari last updated on 27/Oct/20

$${On}\:{Brilliant}\:{app} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Oct/20
https://brilliant.org/problems/functional-complex-trignometry
Commented by Ar Brandon last updated on 27/Oct/20
��OK cool
Answered by TANMAY PANACEA last updated on 27/Oct/20
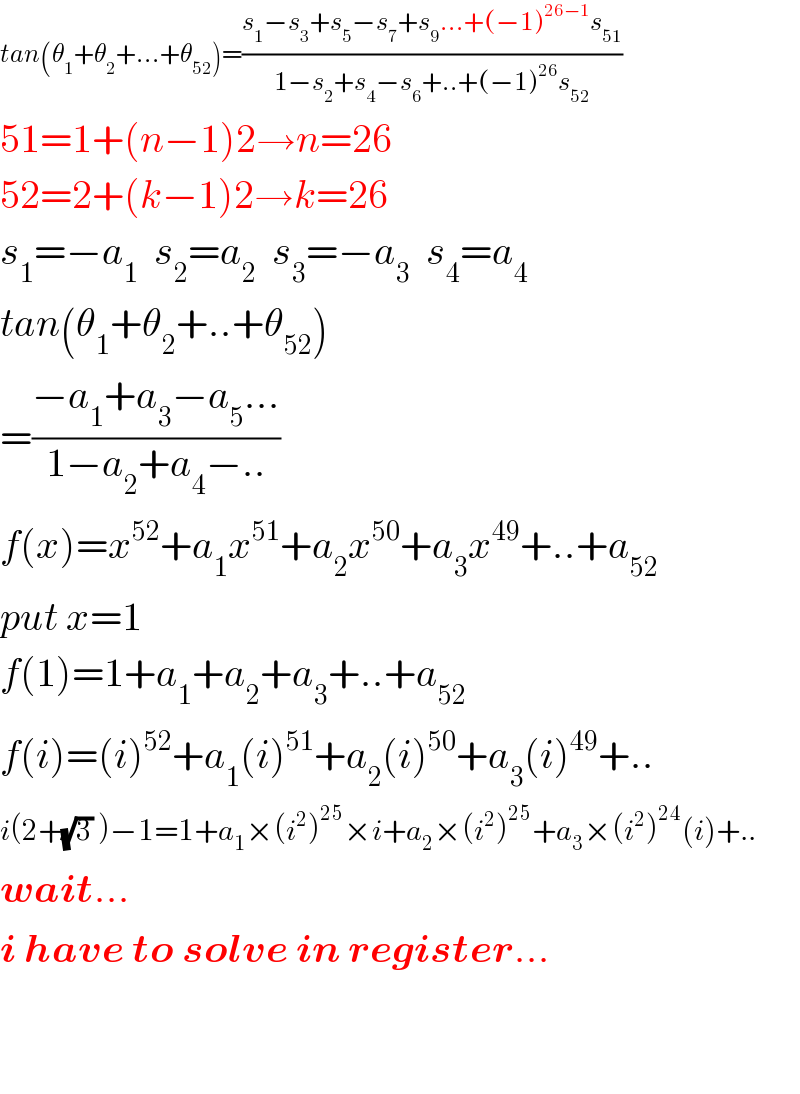
$${tan}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} +…+\theta_{\mathrm{52}} \right)=\frac{{s}_{\mathrm{1}} −{s}_{\mathrm{3}} +{s}_{\mathrm{5}} −{s}_{\mathrm{7}} +{s}_{\mathrm{9}} …+\left(−\mathrm{1}\right)^{\mathrm{26}−\mathrm{1}} {s}_{\mathrm{51}} }{\mathrm{1}−{s}_{\mathrm{2}} +{s}_{\mathrm{4}} −{s}_{\mathrm{6}} +..+\left(−\mathrm{1}\right)^{\mathrm{26}} {s}_{\mathrm{52}} } \\ $$$$\mathrm{51}=\mathrm{1}+\left({n}−\mathrm{1}\right)\mathrm{2}\rightarrow{n}=\mathrm{26} \\ $$$$\mathrm{52}=\mathrm{2}+\left({k}−\mathrm{1}\right)\mathrm{2}\rightarrow{k}=\mathrm{26} \\ $$$${s}_{\mathrm{1}} =−{a}_{\mathrm{1}} \:\:{s}_{\mathrm{2}} ={a}_{\mathrm{2}} \:\:{s}_{\mathrm{3}} =−{a}_{\mathrm{3}} \:\:{s}_{\mathrm{4}} ={a}_{\mathrm{4}} \\ $$$${tan}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} +..+\theta_{\mathrm{52}} \right) \\ $$$$=\frac{−{a}_{\mathrm{1}} +{a}_{\mathrm{3}} −{a}_{\mathrm{5}} …}{\mathrm{1}−{a}_{\mathrm{2}} +{a}_{\mathrm{4}} −..} \\ $$$${f}\left({x}\right)={x}^{\mathrm{52}} +{a}_{\mathrm{1}} {x}^{\mathrm{51}} +{a}_{\mathrm{2}} {x}^{\mathrm{50}} +{a}_{\mathrm{3}} {x}^{\mathrm{49}} +..+{a}_{\mathrm{52}} \\ $$$${put}\:{x}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +..+{a}_{\mathrm{52}} \\ $$$${f}\left({i}\right)=\left({i}\right)^{\mathrm{52}} +{a}_{\mathrm{1}} \left({i}\right)^{\mathrm{51}} +{a}_{\mathrm{2}} \left({i}\right)^{\mathrm{50}} +{a}_{\mathrm{3}} \left({i}\right)^{\mathrm{49}} +.. \\ $$$${i}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)−\mathrm{1}=\mathrm{1}+{a}_{\mathrm{1}} ×\left({i}^{\mathrm{2}} \right)^{\mathrm{25}} ×{i}+{a}_{\mathrm{2}} ×\left({i}^{\mathrm{2}} \right)^{\mathrm{25}} +{a}_{\mathrm{3}} ×\left({i}^{\mathrm{2}} \right)^{\mathrm{24}} \left({i}\right)+.. \\ $$$$\boldsymbol{{wait}}… \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{have}}\:\boldsymbol{{to}}\:\boldsymbol{{solve}}\:\boldsymbol{{in}}\:\boldsymbol{{register}}… \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 27/Oct/20
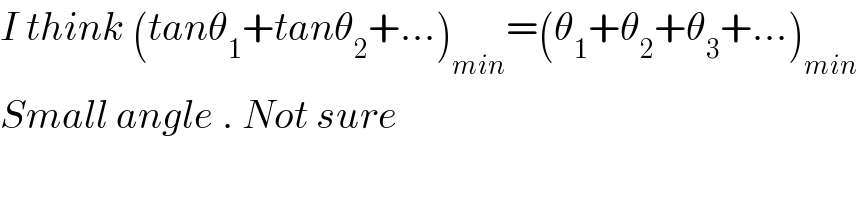
$${I}\:{think}\:\left({tan}\theta_{\mathrm{1}} +{tan}\theta_{\mathrm{2}} +…\right)_{{min}} =\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} +\theta_{\mathrm{3}} +…\right)_{{min}} \\ $$$${Small}\:{angle}\:.\:{Not}\:{sure}\: \\ $$
