Question Number 119892 by peter frank last updated on 27/Oct/20
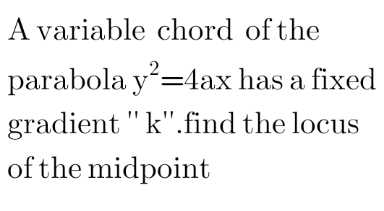
Answered by TANMAY PANACEA last updated on 28/Oct/20
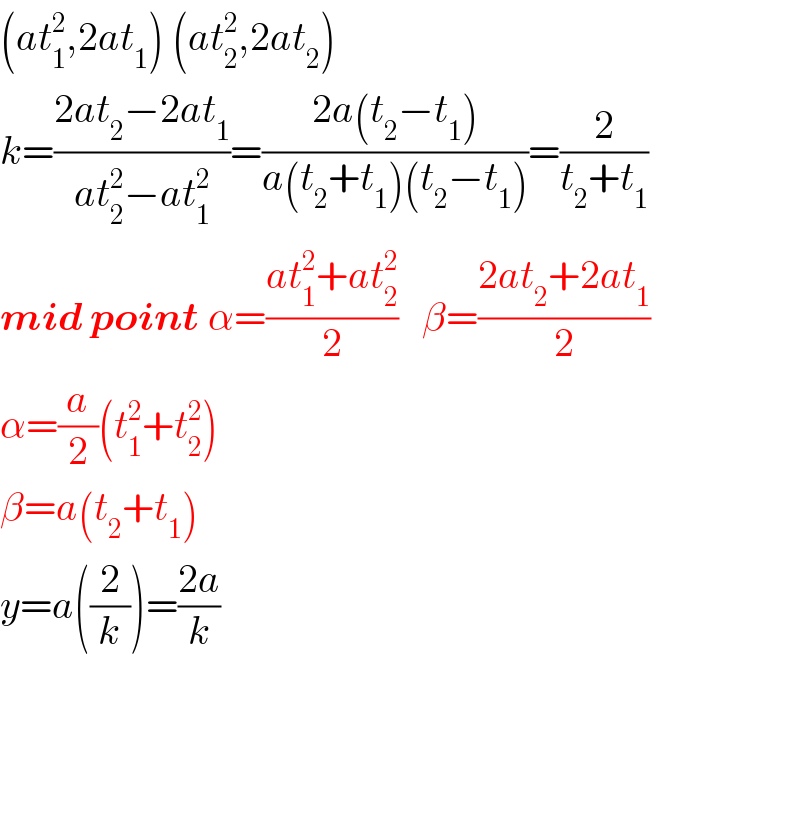
$$\left({at}_{\mathrm{1}} ^{\mathrm{2}} ,\mathrm{2}{at}_{\mathrm{1}} \right)\:\left({at}_{\mathrm{2}} ^{\mathrm{2}} ,\mathrm{2}{at}_{\mathrm{2}} \right) \\ $$$${k}=\frac{\mathrm{2}{at}_{\mathrm{2}} −\mathrm{2}{at}_{\mathrm{1}} }{{at}_{\mathrm{2}} ^{\mathrm{2}} −{at}_{\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{2}{a}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)}{{a}\left({t}_{\mathrm{2}} +{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)}=\frac{\mathrm{2}}{{t}_{\mathrm{2}} +{t}_{\mathrm{1}} } \\ $$$$\boldsymbol{{mid}}\:\boldsymbol{{point}}\:\alpha=\frac{{at}_{\mathrm{1}} ^{\mathrm{2}} +{at}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}}\:\:\:\beta=\frac{\mathrm{2}{at}_{\mathrm{2}} +\mathrm{2}{at}_{\mathrm{1}} }{\mathrm{2}} \\ $$$$\alpha=\frac{{a}}{\mathrm{2}}\left({t}_{\mathrm{1}} ^{\mathrm{2}} +{t}_{\mathrm{2}} ^{\mathrm{2}} \right) \\ $$$$\beta={a}\left({t}_{\mathrm{2}} +{t}_{\mathrm{1}} \right) \\ $$$${y}={a}\left(\frac{\mathrm{2}}{{k}}\right)=\frac{\mathrm{2}{a}}{{k}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 28/Oct/20

$$\mathrm{thank}\:\mathrm{you}. \\ $$
Commented by TANMAY PANACEA last updated on 29/Oct/20

$${most}\:{welcome} \\ $$
