Question-119896

Question Number 119896 by benjo_mathlover last updated on 27/Oct/20

Commented by bobhans last updated on 28/Oct/20

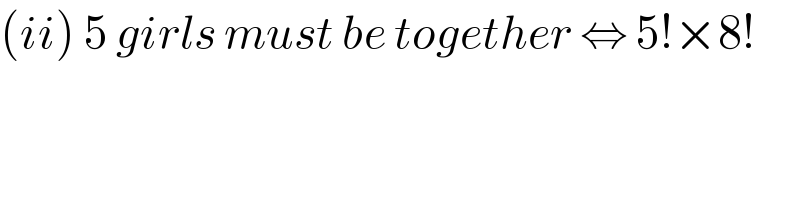
$$\left({ii}\right)\:\mathrm{5}\:{girls}\:{must}\:{be}\:{together}\:\Leftrightarrow\:\mathrm{5}!×\mathrm{8}! \\ $$

Answered by mr W last updated on 28/Oct/20

(i) 12!=479 001 600 (ii) 5!8!=4 838 400 (iii) □G■G■G■G■G□ □=zero or more boys ■=one or more boys (1+x+x^2 +...)^2 (x+x^2 +x^3 +...)^4 =(x^4 /((1−x)^6 ))=x^4 Σ_(k=0) ^∞ C_5 ^(k+5) x^k k=3, C_5 ^8 ⇒C_5 ^8 ×5!×7!=33 868 800 (iv) □AGGGB□ □=zero or more students (1+x+x^2 +...)^2 =(1/((1−x)^2 ))=Σ_(k=0) ^∞ C_1 ^(k+1) x^k k=7, C_1 ^8 ⇒C_1 ^8 ×2!×C_3 ^5 ×3!×7!=4 838 400

$$\left({i}\right) \\ $$$$\mathrm{12}!=\mathrm{479}\:\mathrm{001}\:\mathrm{600} \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$$\mathrm{5}!\mathrm{8}!=\mathrm{4}\:\mathrm{838}\:\mathrm{400} \\ $$$$ \\ $$$$\left({iii}\right) \\ $$$$\Box{G}\blacksquare{G}\blacksquare{G}\blacksquare{G}\blacksquare{G}\Box \\ $$$$\Box={zero}\:{or}\:{more}\:{boys} \\ $$$$\blacksquare={one}\:{or}\:{more}\:{boys} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)^{\mathrm{2}} \left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)^{\mathrm{4}} \\ $$$$=\frac{{x}^{\mathrm{4}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{6}} }={x}^{\mathrm{4}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{5}} ^{{k}+\mathrm{5}} {x}^{{k}} \\ $$$${k}=\mathrm{3},\:{C}_{\mathrm{5}} ^{\mathrm{8}} \\ $$$$\Rightarrow{C}_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{5}!×\mathrm{7}!=\mathrm{33}\:\mathrm{868}\:\mathrm{800} \\ $$$$ \\ $$$$\left({iv}\right) \\ $$$$\Box{AGGGB}\Box \\ $$$$\Box={zero}\:{or}\:{more}\:{students} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{1}} ^{{k}+\mathrm{1}} {x}^{{k}} \\ $$$${k}=\mathrm{7},\:{C}_{\mathrm{1}} ^{\mathrm{8}} \\ $$$$\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{8}} ×\mathrm{2}!×{C}_{\mathrm{3}} ^{\mathrm{5}} ×\mathrm{3}!×\mathrm{7}!=\mathrm{4}\:\mathrm{838}\:\mathrm{400} \\ $$

Commented by Ar Brandon last updated on 28/Oct/20

Thanks for correction, Sir.

Answered by bobhans last updated on 28/Oct/20

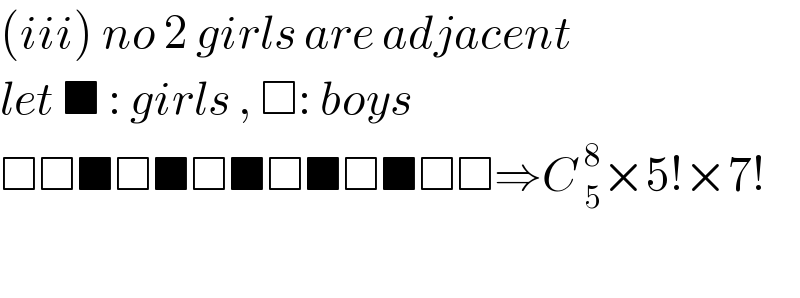
(iii) no 2 girls are adjacent let ■ : girls , □: boys □□■□■□■□■□■□□⇒C _5^8 ×5!×7!

$$\left({iii}\right)\:{no}\:\mathrm{2}\:{girls}\:{are}\:{adjacent} \\ $$$${let}\:\blacksquare\::\:{girls}\:,\:\Box:\:{boys} \\ $$$$\Box\Box\blacksquare\Box\blacksquare\Box\blacksquare\Box\blacksquare\Box\blacksquare\Box\Box\Rightarrow{C}\:_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{5}!×\mathrm{7}! \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply