Menu Close

Question-119928

Tinku Tara 0 Comments
Pin




Question Number 119928 by peter frank last updated on 28/Oct/20
Answered by bramlexs22 last updated on 28/Oct/20
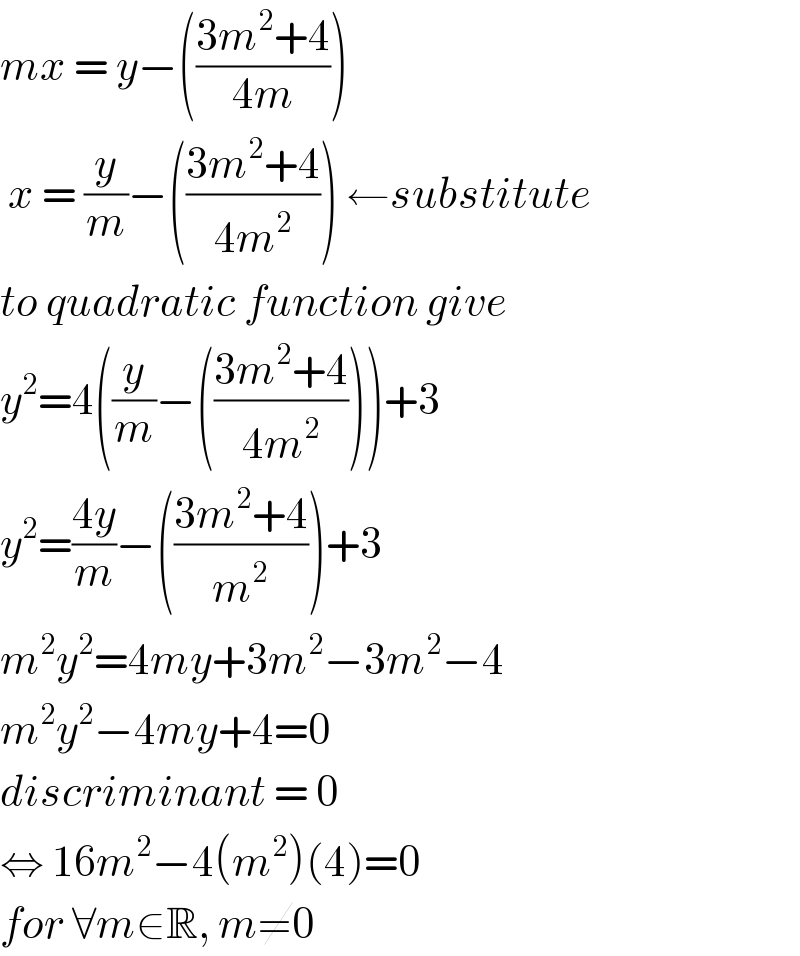
mx = y−(((3m^2 +4)/(4m))) x = (y/m)−(((3m^2 +4)/(4m^2 ))) ←substitute to quadratic function give y^2 =4((y/m)−(((3m^2 +4)/(4m^2 ))))+3 y^2 =((4y)/m)−(((3m^2 +4)/m^2 ))+3 m^2 y^2 =4my+3m^2 −3m^2 −4 m^2 y^2 −4my+4=0 discriminant = 0 ⇔ 16m^2 −4(m^2 )(4)=0 for ∀m∈R, m≠0
$${mx}\:=\:{y}−\left(\frac{\mathrm{3}{m}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}{m}}\right) \\ $$$$\:{x}\:=\:\frac{{y}}{{m}}−\left(\frac{\mathrm{3}{m}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}{m}^{\mathrm{2}} }\right)\:\leftarrow{substitute} \\ $$$${to}\:{quadratic}\:{function}\:{give} \\ $$$${y}^{\mathrm{2}} =\mathrm{4}\left(\frac{{y}}{{m}}−\left(\frac{\mathrm{3}{m}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}{m}^{\mathrm{2}} }\right)\right)+\mathrm{3} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{4}{y}}{{m}}−\left(\frac{\mathrm{3}{m}^{\mathrm{2}} +\mathrm{4}}{{m}^{\mathrm{2}} }\right)+\mathrm{3} \\ $$$${m}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{4}{my}+\mathrm{3}{m}^{\mathrm{2}} −\mathrm{3}{m}^{\mathrm{2}} −\mathrm{4} \\ $$$${m}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{4}{my}+\mathrm{4}=\mathrm{0} \\ $$$${discriminant}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{16}{m}^{\mathrm{2}} −\mathrm{4}\left({m}^{\mathrm{2}} \right)\left(\mathrm{4}\right)=\mathrm{0} \\ $$$${for}\:\forall{m}\in\mathbb{R},\:{m}\neq\mathrm{0} \\ $$
Commented by peter frank last updated on 28/Oct/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by 1549442205PVT last updated on 29/Oct/20
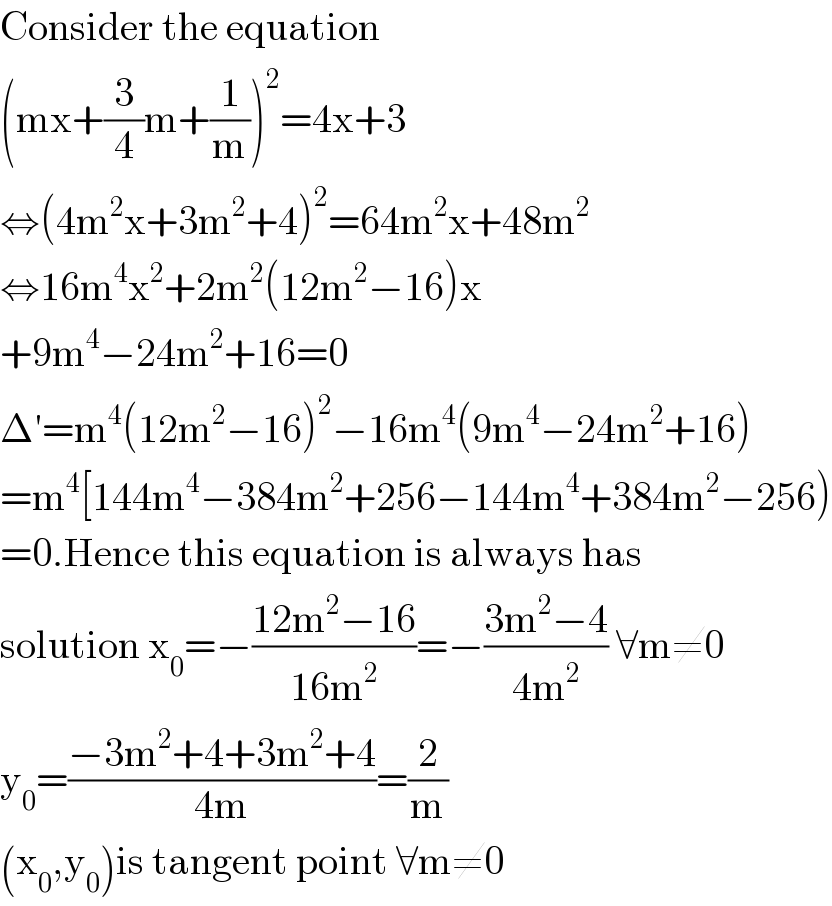
Consider the equation (mx+(3/4)m+(1/m))^2 =4x+3 ⇔(4m^2 x+3m^2 +4)^2 =64m^2 x+48m^2 ⇔16m^4 x^2 +2m^2 (12m^2 −16)x +9m^4 −24m^2 +16=0 Δ′=m^4 (12m^2 −16)^2 −16m^4 (9m^4 −24m^2 +16) =m^4 [144m^4 −384m^2 +256−144m^4 +384m^2 −256) =0.Hence this equation is always has solution x_0 =−((12m^2 −16)/(16m^2 ))=−((3m^2 −4)/(4m^2 )) ∀m≠0 y_0 =((−3m^2 +4+3m^2 +4)/(4m))=(2/m) (x_0 ,y_0 )is tangent point ∀m≠0
$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\left(\mathrm{mx}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{m}+\frac{\mathrm{1}}{\mathrm{m}}\right)^{\mathrm{2}} =\mathrm{4x}+\mathrm{3} \\ $$$$\Leftrightarrow\left(\mathrm{4m}^{\mathrm{2}} \mathrm{x}+\mathrm{3m}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} =\mathrm{64m}^{\mathrm{2}} \mathrm{x}+\mathrm{48m}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{16m}^{\mathrm{4}} \mathrm{x}^{\mathrm{2}} +\mathrm{2m}^{\mathrm{2}} \left(\mathrm{12m}^{\mathrm{2}} −\mathrm{16}\right)\mathrm{x} \\ $$$$+\mathrm{9m}^{\mathrm{4}} −\mathrm{24m}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$$\Delta'=\mathrm{m}^{\mathrm{4}} \left(\mathrm{12m}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{2}} −\mathrm{16m}^{\mathrm{4}} \left(\mathrm{9m}^{\mathrm{4}} −\mathrm{24m}^{\mathrm{2}} +\mathrm{16}\right) \\ $$$$=\mathrm{m}^{\mathrm{4}} \left[\mathrm{144m}^{\mathrm{4}} −\mathrm{384m}^{\mathrm{2}} +\mathrm{256}−\mathrm{144m}^{\mathrm{4}} +\mathrm{384m}^{\mathrm{2}} −\mathrm{256}\right) \\ $$$$=\mathrm{0}.\mathrm{Hence}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{always}\:\mathrm{has} \\ $$$$\mathrm{solution}\:\mathrm{x}_{\mathrm{0}} =−\frac{\mathrm{12m}^{\mathrm{2}} −\mathrm{16}}{\mathrm{16m}^{\mathrm{2}} }=−\frac{\mathrm{3m}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4m}^{\mathrm{2}} }\:\forall\mathrm{m}\neq\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{0}} =\frac{−\mathrm{3m}^{\mathrm{2}} +\mathrm{4}+\mathrm{3m}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4m}}=\frac{\mathrm{2}}{\mathrm{m}} \\ $$$$\left(\mathrm{x}_{\mathrm{0}} ,\mathrm{y}_{\mathrm{0}} \right)\mathrm{is}\:\mathrm{tangent}\:\mathrm{point}\:\forall\mathrm{m}\neq\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *