Question-119960

Question Number 119960 by mnjuly1970 last updated on 28/Oct/20

Answered by mathmax by abdo last updated on 28/Oct/20

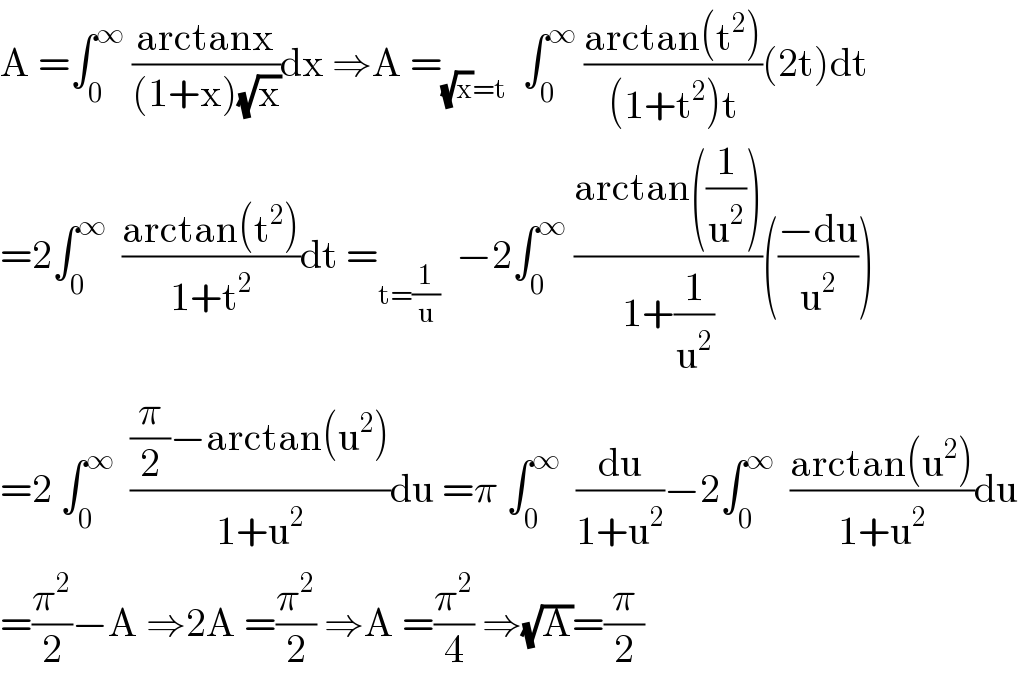
A =∫_0 ^∞ ((arctanx)/((1+x)(√x)))dx ⇒A =_((√x)=t) ∫_0 ^∞ ((arctan(t^2 ))/((1+t^2 )t))(2t)dt =2∫_0 ^∞ ((arctan(t^2 ))/(1+t^2 ))dt =_(t=(1/u)) −2∫_0 ^∞ ((arctan((1/u^2 )))/(1+(1/u^2 )))(((−du)/u^2 )) =2 ∫_0 ^∞ (((π/2)−arctan(u^2 ))/(1+u^2 ))du =π ∫_0 ^∞ (du/(1+u^2 ))−2∫_0 ^∞ ((arctan(u^2 ))/(1+u^2 ))du =(π^2 /2)−A ⇒2A =(π^2 /2) ⇒A =(π^2 /4) ⇒(√A)=(π/2)

$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctanx}}{\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{x}}}\mathrm{dx}\:\Rightarrow\mathrm{A}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}} \:\:−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}\left(\frac{−\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{A}\:\Rightarrow\mathrm{2A}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{A}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\sqrt{\mathrm{A}}=\frac{\pi}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply