Question Number 119965 by sdfg last updated on 28/Oct/20
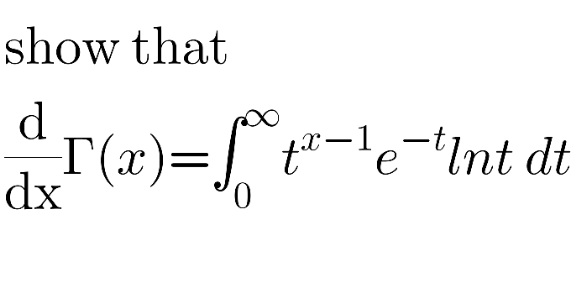
Answered by Dwaipayan Shikari last updated on 28/Oct/20
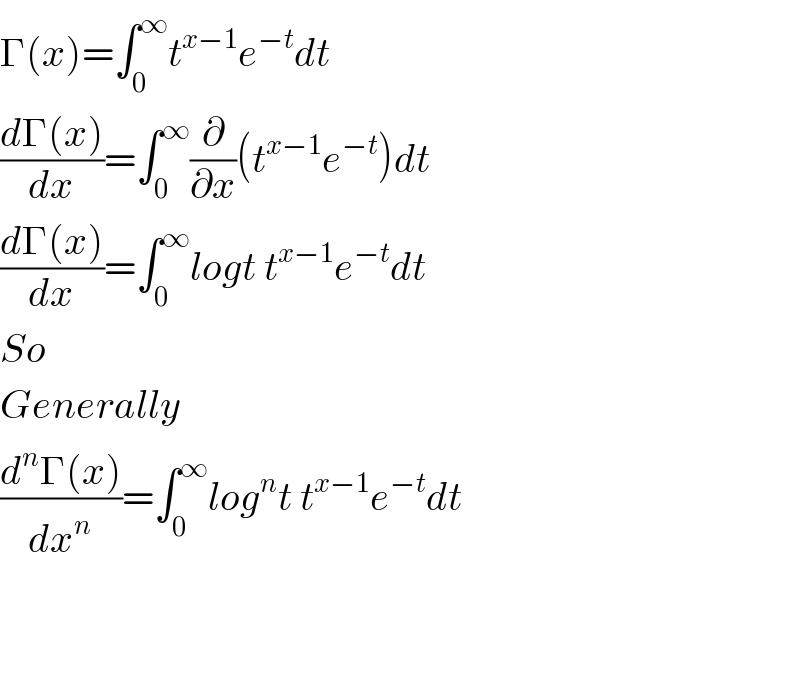
$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\frac{{d}\Gamma\left({x}\right)}{{dx}}=\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial{x}}\left({t}^{{x}−\mathrm{1}} {e}^{−{t}} \right){dt} \\ $$$$\frac{{d}\Gamma\left({x}\right)}{{dx}}=\int_{\mathrm{0}} ^{\infty} {logt}\:{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$${So} \\ $$$${Generally} \\ $$$$\frac{{d}^{{n}} \Gamma\left({x}\right)}{{dx}^{{n}} }=\int_{\mathrm{0}} ^{\infty} {log}^{{n}} {t}\:{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
