Question Number 120127 by huotpat last updated on 29/Oct/20

Answered by Dwaipayan Shikari last updated on 29/Oct/20
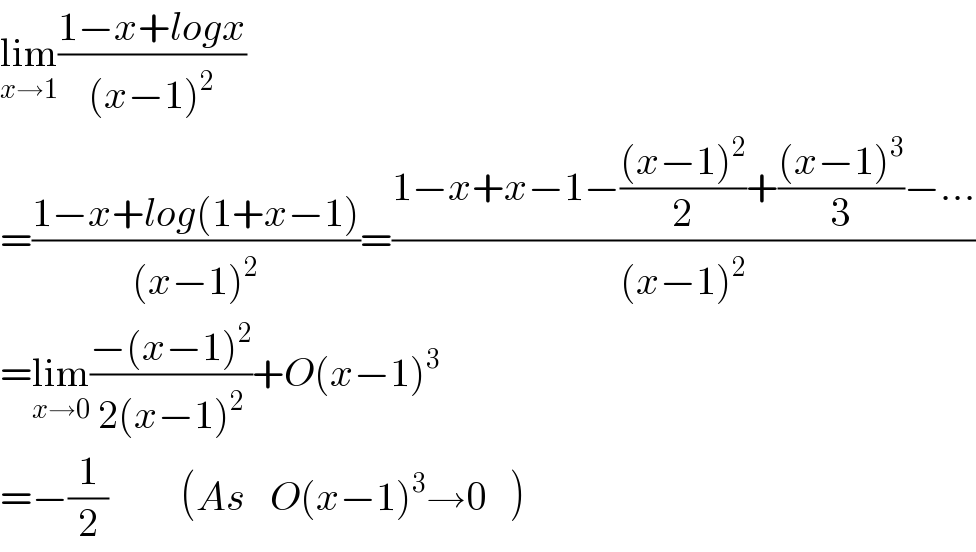
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}−{x}+{logx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−{x}+{log}\left(\mathrm{1}+{x}−\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}−{x}+{x}−\mathrm{1}−\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}−…}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+{O}\left({x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\left({As}\:\:\:{O}\left({x}−\mathrm{1}\right)^{\mathrm{3}} \rightarrow\mathrm{0}\:\:\:\right) \\ $$
Answered by Bird last updated on 29/Oct/20
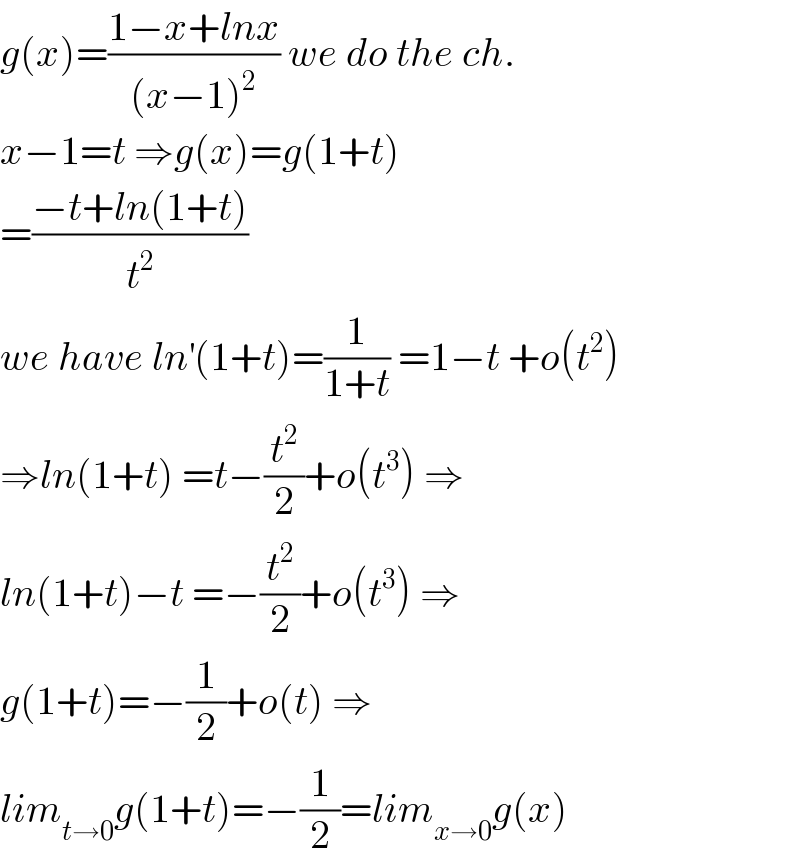
$${g}\left({x}\right)=\frac{\mathrm{1}−{x}+{lnx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{we}\:{do}\:{the}\:{ch}. \\ $$$${x}−\mathrm{1}={t}\:\Rightarrow{g}\left({x}\right)={g}\left(\mathrm{1}+{t}\right) \\ $$$$=\frac{−{t}+{ln}\left(\mathrm{1}+{t}\right)}{{t}^{\mathrm{2}} } \\ $$$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}}\:=\mathrm{1}−{t}\:+{o}\left({t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{t}\right)\:={t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({t}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}\right)−{t}\:=−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({t}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${g}\left(\mathrm{1}+{t}\right)=−\frac{\mathrm{1}}{\mathrm{2}}+{o}\left({t}\right)\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} {g}\left(\mathrm{1}+{t}\right)=−\frac{\mathrm{1}}{\mathrm{2}}={lim}_{{x}\rightarrow\mathrm{0}} {g}\left({x}\right) \\ $$
