Question Number 120322 by sdfg last updated on 30/Oct/20

Commented by TANMAY PANACEA last updated on 30/Oct/20
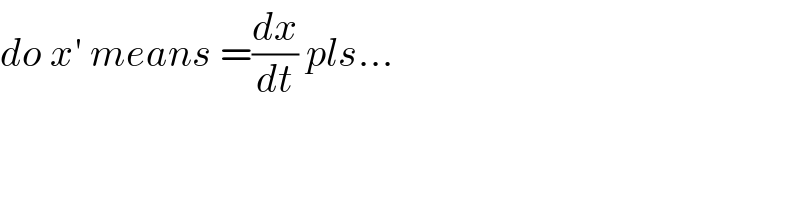
$${do}\:{x}'\:{means}\:=\frac{{dx}}{{dt}}\:{pls}… \\ $$
Commented by Dwaipayan Shikari last updated on 30/Oct/20
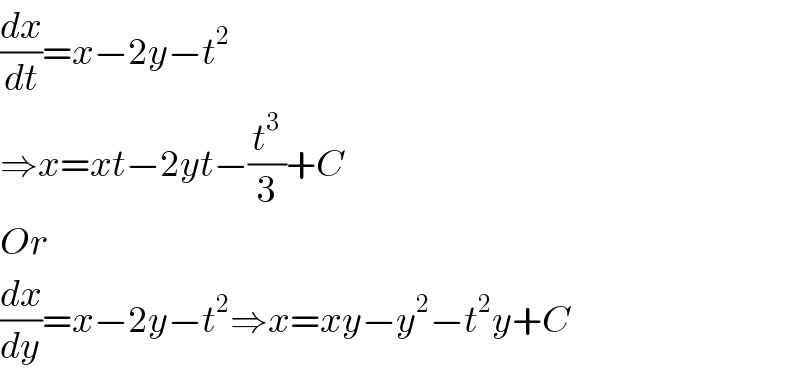
$$\frac{{dx}}{{dt}}={x}−\mathrm{2}{y}−{t}^{\mathrm{2}} \\ $$$$\Rightarrow{x}={xt}−\mathrm{2}{yt}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{C} \\ $$$${Or} \\ $$$$\frac{{dx}}{{dy}}={x}−\mathrm{2}{y}−{t}^{\mathrm{2}} \Rightarrow{x}={xy}−{y}^{\mathrm{2}} −{t}^{\mathrm{2}} {y}+{C} \\ $$
Commented by prakash jain last updated on 31/Oct/20

$$\mathrm{Second}\:\mathrm{Step}: \\ $$$${y}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{or}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:{t}? \\ $$
Answered by mr W last updated on 31/Oct/20
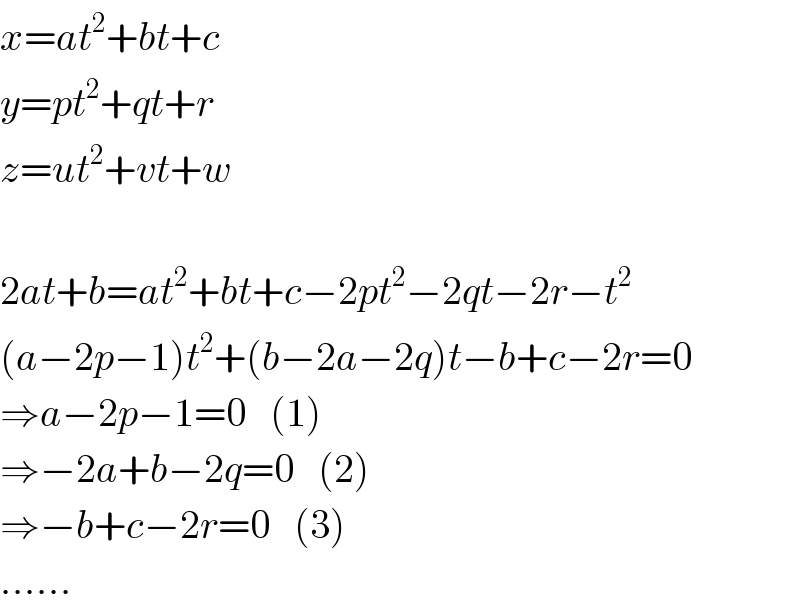
$${x}={at}^{\mathrm{2}} +{bt}+{c} \\ $$$${y}={pt}^{\mathrm{2}} +{qt}+{r} \\ $$$${z}={ut}^{\mathrm{2}} +{vt}+{w} \\ $$$$ \\ $$$$\mathrm{2}{at}+{b}={at}^{\mathrm{2}} +{bt}+{c}−\mathrm{2}{pt}^{\mathrm{2}} −\mathrm{2}{qt}−\mathrm{2}{r}−{t}^{\mathrm{2}} \\ $$$$\left({a}−\mathrm{2}{p}−\mathrm{1}\right){t}^{\mathrm{2}} +\left({b}−\mathrm{2}{a}−\mathrm{2}{q}\right){t}−{b}+{c}−\mathrm{2}{r}=\mathrm{0} \\ $$$$\Rightarrow{a}−\mathrm{2}{p}−\mathrm{1}=\mathrm{0}\:\:\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow−\mathrm{2}{a}+{b}−\mathrm{2}{q}=\mathrm{0}\:\:\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow−{b}+{c}−\mathrm{2}{r}=\mathrm{0}\:\:\:\left(\mathrm{3}\right) \\ $$$$…… \\ $$
