Question Number 120438 by bramlexs22 last updated on 31/Oct/20
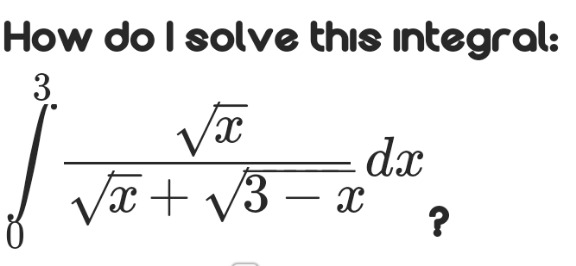
Answered by TANMAY PANACEA last updated on 31/Oct/20

$${formula} \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\sqrt{\mathrm{3}−{x}}}{\:\sqrt{\mathrm{3}−{x}}\:+\sqrt{\mathrm{3}−\left(\mathrm{3}−{x}\right)}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\sqrt{\mathrm{3}−{x}}}{\:\sqrt{\mathrm{3}−{x}}\:+\sqrt{{x}}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\frac{\sqrt{{x}}}{\:\sqrt{{x}}\:+\sqrt{\mathrm{3}−{x}}}+\frac{\sqrt{\mathrm{3}−{x}}}{\:\sqrt{\mathrm{3}−{x}}\:+\sqrt{{x}}}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}×\mid{x}\mid_{\mathrm{0}} ^{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Answered by john santu last updated on 31/Oct/20
![letting 3−x = ϑ ⇒ { ((x=0→ϑ=3)),((x=3→ϑ=0)) :} I = ∫_0 ^3 ((√x)/( (√x)+(√(3−x)))) dx = ∫_3 ^0 ((√(3−ϑ))/( (√(3−ϑ))+(√ϑ))) (−dϑ) 2I = ∫_0 ^3 (((√x) +(√(3−x)))/( (√x)+(√(3−x)) )) dx = ∫_0 ^3 dx 2I = [ x ]_0 ^3 = 3 ⇒I = 1.5](https://www.tinkutara.com/question/Q120442.png)
$$\:{letting}\:\mathrm{3}−{x}\:=\:\vartheta\:\Rightarrow\begin{cases}{{x}=\mathrm{0}\rightarrow\vartheta=\mathrm{3}}\\{{x}=\mathrm{3}\rightarrow\vartheta=\mathrm{0}}\end{cases} \\ $$$${I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{\sqrt{{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{3}−{x}}}\:{dx}\:=\:\underset{\mathrm{3}} {\overset{\mathrm{0}} {\int}}\:\frac{\sqrt{\mathrm{3}−\vartheta}}{\:\sqrt{\mathrm{3}−\vartheta}+\sqrt{\vartheta}}\:\left(−{d}\vartheta\right) \\ $$$$\mathrm{2}{I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{\sqrt{{x}}\:+\sqrt{\mathrm{3}−{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{3}−{x}}\:}\:{dx}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:{dx} \\ $$$$\mathrm{2}{I}\:=\:\left[\:{x}\:\right]_{\mathrm{0}} ^{\mathrm{3}} \:=\:\mathrm{3}\:\Rightarrow{I}\:=\:\mathrm{1}.\mathrm{5} \\ $$
Answered by som(math1967) last updated on 31/Oct/20
![I=∫^3 _0 ((√(3+0−x))/( (√(3+0−x))+(√(3−(3+0−x))))dx =∫_0 ^3 ((√(3−x))/( (√(3−x))+(√x)))dx ∴2I=∫_0 ^3 ((√(3−x))/( (√(3−x))+(√x)))dx+∫_0 ^3 ((√x)/( (√x)+(√(3−x))))dx =∫_0 ^3 (((√(3−x))+(√x))/( (√(3−x))+(√x)))dx =∫_0 ^3 dx=[x]^3 _0 =3−0=3 ∴I=(3/2)ans](https://www.tinkutara.com/question/Q120443.png)
$$\mathrm{I}=\underset{\mathrm{0}} {\int}^{\mathrm{3}} \frac{\sqrt{\mathrm{3}+\mathrm{0}−\mathrm{x}}}{\:\sqrt{\mathrm{3}+\mathrm{0}−\mathrm{x}}+\sqrt{\mathrm{3}−\left(\mathrm{3}+\mathrm{0}−\mathrm{x}\right.}}\mathrm{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\sqrt{\mathrm{3}−\mathrm{x}}}{\:\sqrt{\mathrm{3}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$\therefore\mathrm{2I}=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\sqrt{\mathrm{3}−\mathrm{x}}}{\:\sqrt{\mathrm{3}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}+\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}}+\sqrt{\mathrm{3}−\mathrm{x}}}\mathrm{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\sqrt{\mathrm{3}−\mathrm{x}}+\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{3}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{dx}=\left[\mathrm{x}\underset{\mathrm{0}} {\right]}^{\mathrm{3}} =\mathrm{3}−\mathrm{0}=\mathrm{3}\: \\ $$$$\therefore\mathrm{I}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ans} \\ $$
