Question Number 120464 by pooooop last updated on 31/Oct/20
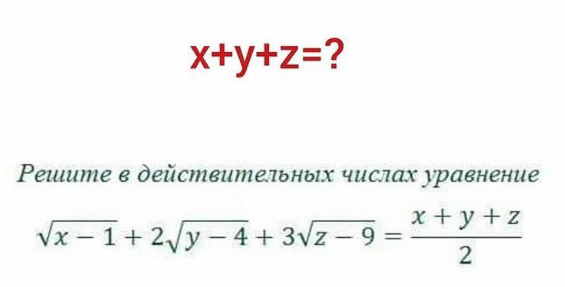
Answered by Jamshidbek2311 last updated on 31/Oct/20
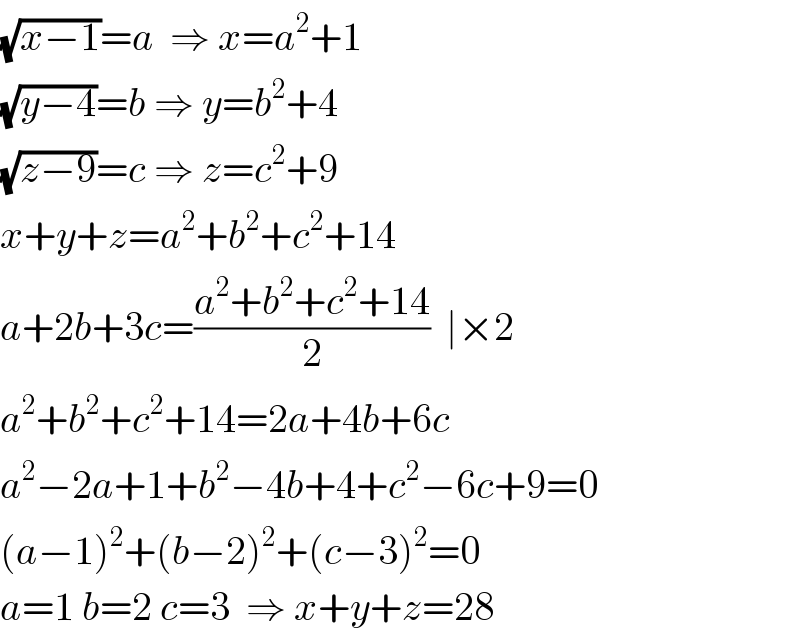
$$\sqrt{{x}−\mathrm{1}}={a}\:\:\Rightarrow\:{x}={a}^{\mathrm{2}} +\mathrm{1} \\ $$$$\sqrt{{y}−\mathrm{4}}={b}\:\Rightarrow\:{y}={b}^{\mathrm{2}} +\mathrm{4} \\ $$$$\sqrt{{z}−\mathrm{9}}={c}\:\Rightarrow\:{z}={c}^{\mathrm{2}} +\mathrm{9}\: \\ $$$${x}+{y}+{z}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{14} \\ $$$${a}+\mathrm{2}{b}+\mathrm{3}{c}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{14}}{\mathrm{2}}\:\:\mid×\mathrm{2} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{14}=\mathrm{2}{a}+\mathrm{4}{b}+\mathrm{6}{c} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}+{b}^{\mathrm{2}} −\mathrm{4}{b}+\mathrm{4}+{c}^{\mathrm{2}} −\mathrm{6}{c}+\mathrm{9}=\mathrm{0} \\ $$$$\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\left({b}−\mathrm{2}\right)^{\mathrm{2}} +\left({c}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${a}=\mathrm{1}\:{b}=\mathrm{2}\:{c}=\mathrm{3}\:\:\Rightarrow\:{x}+{y}+{z}=\mathrm{28} \\ $$
