Question Number 120468 by help last updated on 31/Oct/20
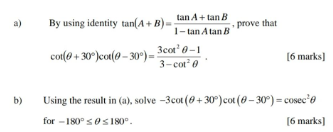
Commented by bemath last updated on 01/Nov/20
![cot (θ+30°) cot (θ−30°)= (1/(tan (θ+30°) tan (θ−30°))) = (1/((((tan θ+((√3)/3))/(1−(((√3) tan θ)/3))) . ((tan θ−((√3)/3))/(1+(((√3) tan θ)/3)))))) = ((1−(1/3)tan^2 θ)/(tan^2 θ−(1/3))) = ((3−tan^2 θ)/(3tan^2 θ−1)) : [ ((tan^2 θ)/(tan^2 θ)) ] = ((3cot^2 θ−1)/(3−cot^2 θ))](https://www.tinkutara.com/question/Q120517.png)
$$\mathrm{cot}\:\left(\theta+\mathrm{30}°\right)\:\mathrm{cot}\:\left(\theta−\mathrm{30}°\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\left(\theta+\mathrm{30}°\right)\:\mathrm{tan}\:\left(\theta−\mathrm{30}°\right)}\:= \\ $$$$\frac{\mathrm{1}}{\left(\frac{\mathrm{tan}\:\theta+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}\:\mathrm{tan}\:\theta}{\mathrm{3}}}\:.\:\frac{\mathrm{tan}\:\theta−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}{\mathrm{1}+\frac{\sqrt{\mathrm{3}}\:\mathrm{tan}\:\theta}{\mathrm{3}}}\right)}\:= \\ $$$$\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:^{\mathrm{2}} \theta}{\mathrm{tan}\:^{\mathrm{2}} \theta−\frac{\mathrm{1}}{\mathrm{3}}}\:=\:\frac{\mathrm{3}−\mathrm{tan}\:^{\mathrm{2}} \theta}{\mathrm{3tan}\:^{\mathrm{2}} \theta−\mathrm{1}}\::\:\left[\:\frac{\mathrm{tan}\:^{\mathrm{2}} \theta}{\mathrm{tan}\:^{\mathrm{2}} \theta}\:\right] \\ $$$$=\:\frac{\mathrm{3cot}\:^{\mathrm{2}} \theta−\mathrm{1}}{\mathrm{3}−\mathrm{cot}\:^{\mathrm{2}} \theta} \\ $$$$ \\ $$
Commented by bemath last updated on 01/Nov/20
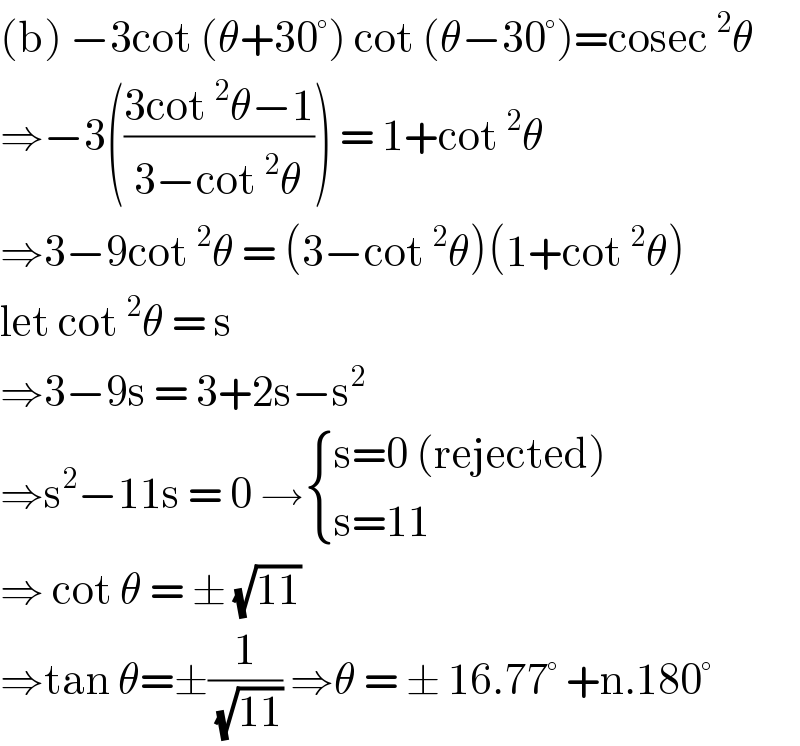
$$\left(\mathrm{b}\right)\:−\mathrm{3cot}\:\left(\theta+\mathrm{30}°\right)\:\mathrm{cot}\:\left(\theta−\mathrm{30}°\right)=\mathrm{cosec}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow−\mathrm{3}\left(\frac{\mathrm{3cot}\:^{\mathrm{2}} \theta−\mathrm{1}}{\mathrm{3}−\mathrm{cot}\:^{\mathrm{2}} \theta}\right)\:=\:\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\mathrm{3}−\mathrm{9cot}\:^{\mathrm{2}} \theta\:=\:\left(\mathrm{3}−\mathrm{cot}\:^{\mathrm{2}} \theta\right)\left(\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} \theta\right) \\ $$$$\mathrm{let}\:\mathrm{cot}\:^{\mathrm{2}} \theta\:=\:\mathrm{s}\: \\ $$$$\Rightarrow\mathrm{3}−\mathrm{9s}\:=\:\mathrm{3}+\mathrm{2s}−\mathrm{s}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{s}^{\mathrm{2}} −\mathrm{11s}\:=\:\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{s}=\mathrm{0}\:\left(\mathrm{rejected}\right)}\\{\mathrm{s}=\mathrm{11}}\end{cases} \\ $$$$\Rightarrow\:\mathrm{cot}\:\theta\:=\:\pm\:\sqrt{\mathrm{11}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\:\Rightarrow\theta\:=\:\pm\:\mathrm{16}.\mathrm{77}°\:+\mathrm{n}.\mathrm{180}° \\ $$
