Question Number 120534 by help last updated on 01/Nov/20

Commented by john santu last updated on 01/Nov/20
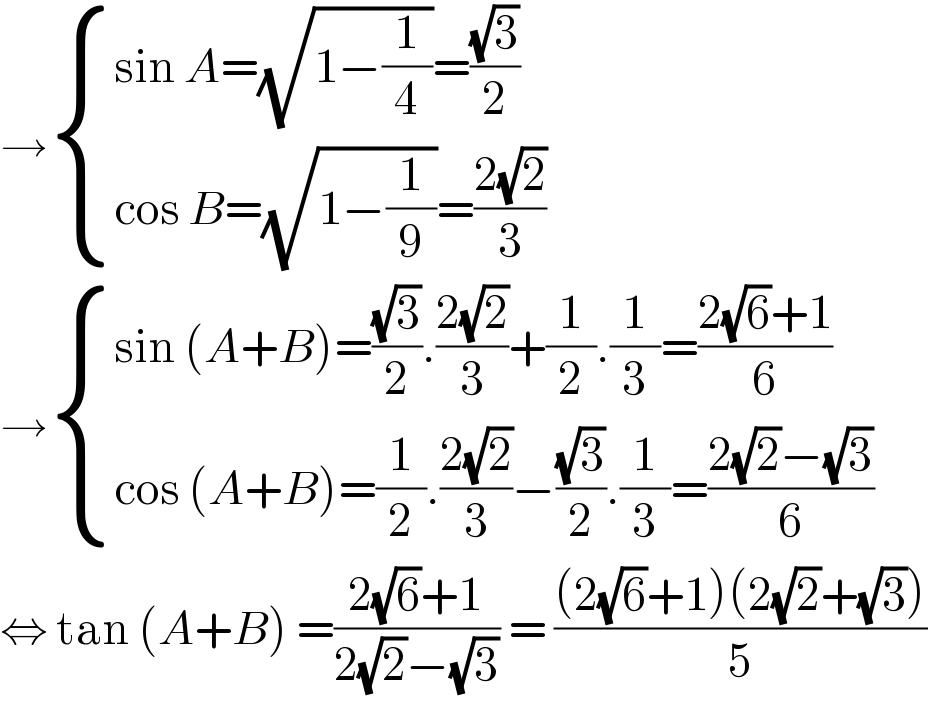
$$\rightarrow\begin{cases}{\mathrm{sin}\:{A}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\mathrm{cos}\:{B}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}}\end{cases} \\ $$$$\rightarrow\begin{cases}{\mathrm{sin}\:\left({A}+{B}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{1}}{\mathrm{6}}}\\{\mathrm{cos}\:\left({A}+{B}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}}{\mathrm{6}}}\end{cases} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\left({A}+{B}\right)\:=\frac{\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}}\:=\:\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)}{\mathrm{5}} \\ $$
Answered by TANMAY PANACEA last updated on 01/Nov/20

$${Better}\:{use}\:{your}\:{brain}… \\ $$$${tanA}=\frac{\sqrt{\mathrm{3}}}{\mathrm{1}}\:\:{tanB}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${tan}\left({A}+{B}\right)=\frac{{tanA}+{tanB}}{\mathrm{1}−{tanAtanB}}=\frac{\sqrt{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}\:+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\:}=\frac{\left.\left(\mathrm{2}\sqrt{\mathrm{6}}\:+\mathrm{1}\right)\left(\right)\mathrm{2}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:\right)}{\mathrm{8}−\mathrm{3}} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{12}}\:+\mathrm{2}\sqrt{\mathrm{18}}\:+\mathrm{2}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}}{\mathrm{5}}=\frac{\mathrm{8}\sqrt{\mathrm{3}}\:+\mathrm{6}\sqrt{\mathrm{2}}\:+\mathrm{2}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}}{\mathrm{5}}=\frac{\mathrm{9}\sqrt{\mathrm{3}}\:+\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$
Answered by Dwaipayan Shikari last updated on 01/Nov/20

$${cosA}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${tanA}=\sqrt{\mathrm{3}} \\ $$$${sinB}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{cosB}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}}\:=\frac{\sqrt{\mathrm{8}}}{\mathrm{3}}\Rightarrow{secB}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{8}}} \\ $$$${tanB}=\sqrt{\frac{\mathrm{9}}{\mathrm{8}}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${tan}\left({A}+{B}\right)=\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}+\sqrt{\mathrm{3}}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}}=\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)}{\mathrm{5}} \\ $$$$=\frac{\mathrm{9}\sqrt{\mathrm{3}}+\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$
