Question Number 120541 by 77731 last updated on 01/Nov/20

Answered by snipers237 last updated on 01/Nov/20
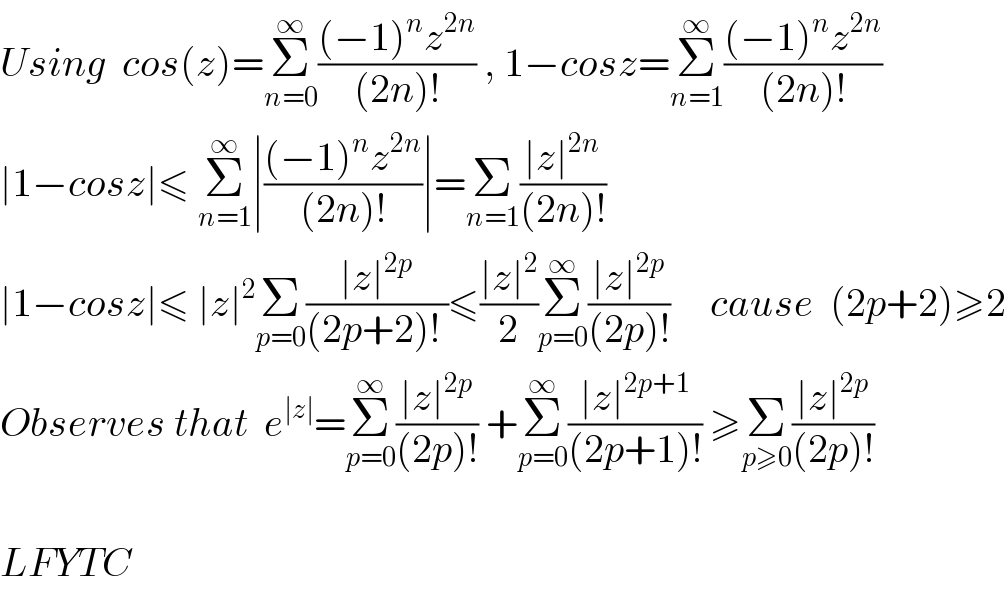
$${Using}\:\:{cos}\left({z}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {z}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:,\:\mathrm{1}−{cosz}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {z}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\: \\ $$$$\mid\mathrm{1}−{cosz}\mid\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mid\frac{\left(−\mathrm{1}\right)^{{n}} {z}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\mid=\underset{{n}=\mathrm{1}} {\sum}\frac{\mid{z}\mid^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$\mid\mathrm{1}−{cosz}\mid\leqslant\:\mid{z}\mid^{\mathrm{2}} \underset{{p}=\mathrm{0}} {\sum}\frac{\mid{z}\mid^{\mathrm{2}{p}} }{\left(\mathrm{2}{p}+\mathrm{2}\right)!\:}\leqslant\frac{\mid{z}\mid^{\mathrm{2}} }{\mathrm{2}}\underset{{p}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mid{z}\mid^{\mathrm{2}{p}} }{\left(\mathrm{2}{p}\right)!}\:\:\:\:\:{cause}\:\:\left(\mathrm{2}{p}+\mathrm{2}\right)\geqslant\mathrm{2} \\ $$$${Observes}\:{that}\:\:{e}^{\mid{z}\mid} =\underset{{p}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mid{z}\mid^{\mathrm{2}{p}} }{\left(\mathrm{2}{p}\right)!}\:+\underset{{p}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mid{z}\mid^{\mathrm{2}{p}+\mathrm{1}} }{\left(\mathrm{2}{p}+\mathrm{1}\right)!}\:\geqslant\underset{{p}\geqslant\mathrm{0}} {\sum}\frac{\mid{z}\mid^{\mathrm{2}{p}} }{\left(\mathrm{2}{p}\right)!} \\ $$$$ \\ $$$${LFYTC} \\ $$
