Question Number 120619 by help last updated on 01/Nov/20

Answered by TANMAY PANACEA last updated on 01/Nov/20
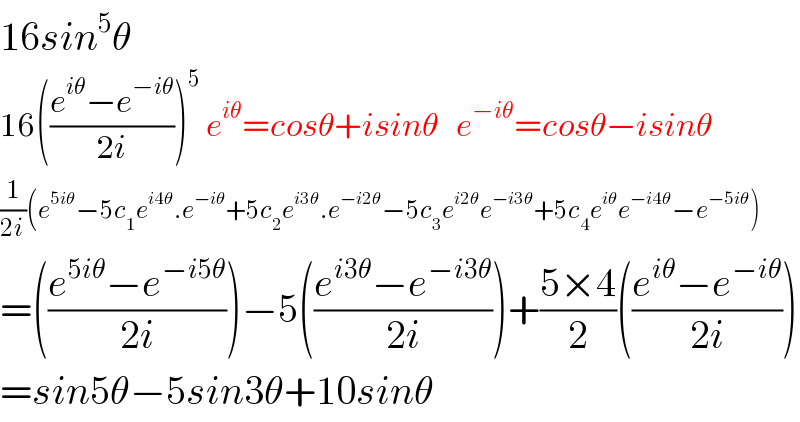
$$\mathrm{16}{sin}^{\mathrm{5}} \theta \\ $$$$\mathrm{16}\left(\frac{{e}^{{i}\theta} −{e}^{−{i}\theta} }{\mathrm{2}{i}}\right)^{\mathrm{5}} \:{e}^{{i}\theta} ={cos}\theta+{isin}\theta\:\:\:{e}^{−{i}\theta} ={cos}\theta−{isin}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{i}}\left({e}^{\mathrm{5}{i}\theta} −\mathrm{5}{c}_{\mathrm{1}} {e}^{{i}\mathrm{4}\theta} .{e}^{−{i}\theta} +\mathrm{5}{c}_{\mathrm{2}} {e}^{{i}\mathrm{3}\theta} .{e}^{−{i}\mathrm{2}\theta} −\mathrm{5}{c}_{\mathrm{3}} {e}^{{i}\mathrm{2}\theta} {e}^{−{i}\mathrm{3}\theta} +\mathrm{5}{c}_{\mathrm{4}} {e}^{{i}\theta} {e}^{−{i}\mathrm{4}\theta} −{e}^{−\mathrm{5}{i}\theta} \right) \\ $$$$=\left(\frac{{e}^{\mathrm{5}{i}\theta} −{e}^{−{i}\mathrm{5}\theta} }{\mathrm{2}{i}}\right)−\mathrm{5}\left(\frac{{e}^{{i}\mathrm{3}\theta} −{e}^{−{i}\mathrm{3}\theta} }{\mathrm{2}{i}}\right)+\frac{\mathrm{5}×\mathrm{4}}{\mathrm{2}}\left(\frac{{e}^{{i}\theta} −{e}^{−{i}\theta} }{\mathrm{2}{i}}\right) \\ $$$$={sin}\mathrm{5}\theta−\mathrm{5}{sin}\mathrm{3}\theta+\mathrm{10}{sin}\theta \\ $$
Commented by peter frank last updated on 01/Nov/20

$$\mathrm{good} \\ $$
