Menu Close

Question-120748

Tinku Tara 0 Comments
Pin




Question Number 120748 by help last updated on 02/Nov/20
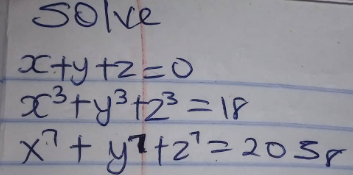
Answered by TANMAY PANACEA last updated on 02/Nov/20
x=3 y=−2 z=−1
$${x}=\mathrm{3}\:\:{y}=−\mathrm{2}\:\:{z}=−\mathrm{1} \\ $$
Commented by help last updated on 02/Nov/20
solution please
$${solution}\:{please} \\ $$
Answered by mindispower last updated on 02/Nov/20
ke_k =Σ_(i=1) ^k (−1)^(i−1) e_(k−i) p_i Newtoon identities e_k =Σ_(1≤a_1 .....a_k ≤n) X_a_1 .....X_a_k ...p_k =Σ_(i=1) ^n X_i ^k 2e_2 =e_1 p_1 −e_0 p_2 ⇒2e_2 =−p_2 3e_3 =e_2 p_1 −e_1 p_2 +p_3 ⇒e_3 =6 0=e_3 p_1 −e_2 p_2 +e_3 p_1 −p_4 =2e_2 ^2 −p_4 p_4 =2e_2 ^2 0=e_4 p_1 −e_3 p_2 +e_2 p_3 −e_1 p_4 +p_5 =−6p_2 +18e_2 +p_5 ⇒p_5 =−30e_2 0=e_5 p_1 −e_4 p_2 +e_3 p_3 −e_2 p_4 +e_1 p_5 −p_6 p_6 =108−2e_2 ^3 7e_7 =e_6 p_1 −e_5 p_2 +e_4 p_3 −e_3 p_4 +e_2 p_5 −e_1 p_6 +p_7 0=−6p_4 +e_2 (−30e_2 )+p_7 −42e_2 ^2 =−2058⇒e_2 =+_− (√((2058)/(42))) =+_− (√(49))=+_− 7 e_2 =7,e_1 =0,e_3 =6 X^3 +7X−6 cardan e_2 =−7 ⇒X^3 −7X−6,X=−1solution (X+1)(X^2 −X−6)⇒X∈{−1,3,−2} (x,y,z)∈{(−1,3,−2)} withe permutation
$${ke}_{{k}} =\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\left(−\mathrm{1}\right)^{{i}−\mathrm{1}} {e}_{{k}−{i}} {p}_{{i}} \\ $$$${Newtoon}\:{identities} \\ $$$${e}_{{k}} =\underset{\mathrm{1}\leqslant{a}_{\mathrm{1}} …..{a}_{{k}} \leqslant{n}} {\sum}{X}_{{a}_{\mathrm{1}} } …..{X}_{{a}_{{k}} } …{p}_{{k}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{X}_{{i}} ^{{k}} \\ $$$$\mathrm{2}{e}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −{e}_{\mathrm{0}} {p}_{\mathrm{2}} \Rightarrow\mathrm{2}{e}_{\mathrm{2}} =−{p}_{\mathrm{2}} \\ $$$$\mathrm{3}{e}_{\mathrm{3}} ={e}_{\mathrm{2}} {p}_{\mathrm{1}} −{e}_{\mathrm{1}} {p}_{\mathrm{2}} +{p}_{\mathrm{3}} \Rightarrow{e}_{\mathrm{3}} =\mathrm{6} \\ $$$$\mathrm{0}={e}_{\mathrm{3}} {p}_{\mathrm{1}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{1}} −{p}_{\mathrm{4}} =\mathrm{2}{e}_{\mathrm{2}} ^{\mathrm{2}} −{p}_{\mathrm{4}} \\ $$$${p}_{\mathrm{4}} =\mathrm{2}{e}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\mathrm{0}={e}_{\mathrm{4}} {p}_{\mathrm{1}} −{e}_{\mathrm{3}} {p}_{\mathrm{2}} +{e}_{\mathrm{2}} {p}_{\mathrm{3}} −{e}_{\mathrm{1}} {p}_{\mathrm{4}} +{p}_{\mathrm{5}} \\ $$$$=−\mathrm{6}{p}_{\mathrm{2}} +\mathrm{18}{e}_{\mathrm{2}} +{p}_{\mathrm{5}} \Rightarrow{p}_{\mathrm{5}} =−\mathrm{30}{e}_{\mathrm{2}} \\ $$$$\mathrm{0}={e}_{\mathrm{5}} {p}_{\mathrm{1}} −{e}_{\mathrm{4}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{4}} +{e}_{\mathrm{1}} {p}_{\mathrm{5}} −{p}_{\mathrm{6}} \\ $$$${p}_{\mathrm{6}} =\mathrm{108}−\mathrm{2}{e}_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\mathrm{7}{e}_{\mathrm{7}} ={e}_{\mathrm{6}} {p}_{\mathrm{1}} −{e}_{\mathrm{5}} {p}_{\mathrm{2}} +{e}_{\mathrm{4}} {p}_{\mathrm{3}} −{e}_{\mathrm{3}} {p}_{\mathrm{4}} +{e}_{\mathrm{2}} {p}_{\mathrm{5}} −{e}_{\mathrm{1}} {p}_{\mathrm{6}} +{p}_{\mathrm{7}} \\ $$$$\mathrm{0}=−\mathrm{6}{p}_{\mathrm{4}} +{e}_{\mathrm{2}} \left(−\mathrm{30}{e}_{\mathrm{2}} \right)+{p}_{\mathrm{7}} \\ $$$$−\mathrm{42}{e}_{\mathrm{2}} ^{\mathrm{2}} =−\mathrm{2058}\Rightarrow{e}_{\mathrm{2}} =\underset{−} {+}\sqrt{\frac{\mathrm{2058}}{\mathrm{42}}} \\ $$$$=\underset{−} {+}\sqrt{\mathrm{49}}=\underset{−} {+}\mathrm{7} \\ $$$${e}_{\mathrm{2}} =\mathrm{7},{e}_{\mathrm{1}} =\mathrm{0},{e}_{\mathrm{3}} =\mathrm{6} \\ $$$${X}^{\mathrm{3}} +\mathrm{7}{X}−\mathrm{6} \\ $$$${cardan} \\ $$$${e}_{\mathrm{2}} =−\mathrm{7} \\ $$$$\Rightarrow{X}^{\mathrm{3}} −\mathrm{7}{X}−\mathrm{6},{X}=−\mathrm{1}{solution} \\ $$$$\left({X}+\mathrm{1}\right)\left({X}^{\mathrm{2}} −{X}−\mathrm{6}\right)\Rightarrow{X}\in\left\{−\mathrm{1},\mathrm{3},−\mathrm{2}\right\} \\ $$$$\left({x},{y},{z}\right)\in\left\{\left(−\mathrm{1},\mathrm{3},−\mathrm{2}\right)\right\}\:{withe}\:{permutation} \\ $$
Commented by help last updated on 02/Nov/20
Gave kudos
$${Gave}\:{kudos} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *