Question Number 120773 by shaker last updated on 02/Nov/20

Answered by 675480065 last updated on 02/Nov/20
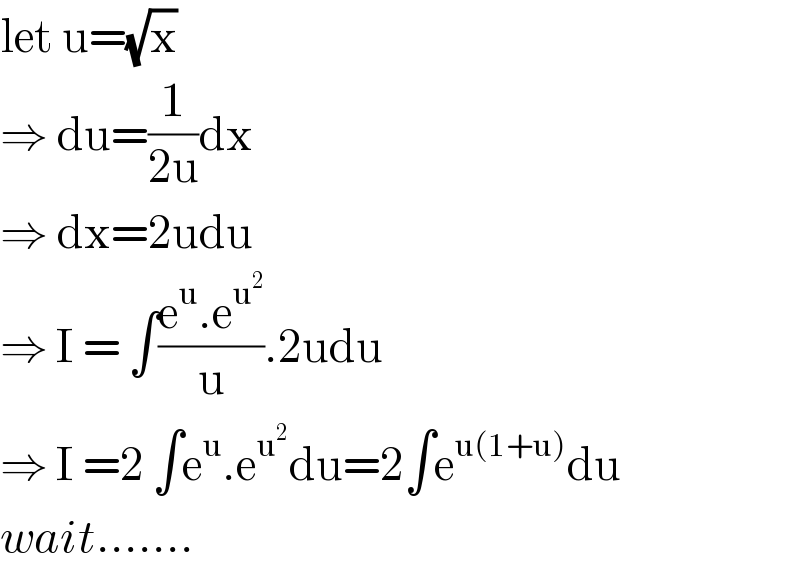
$$\mathrm{let}\:\mathrm{u}=\sqrt{\mathrm{x}} \\ $$$$\Rightarrow\:\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2u}}\mathrm{dx} \\ $$$$\Rightarrow\:\mathrm{dx}=\mathrm{2udu} \\ $$$$\Rightarrow\:\mathrm{I}\:=\:\int\frac{\mathrm{e}^{\mathrm{u}} .\mathrm{e}^{\mathrm{u}^{\mathrm{2}} } }{\mathrm{u}}.\mathrm{2udu} \\ $$$$\Rightarrow\:\mathrm{I}\:=\mathrm{2}\:\int\mathrm{e}^{\mathrm{u}} .\mathrm{e}^{\mathrm{u}^{\mathrm{2}} } \mathrm{du}=\mathrm{2}\int\mathrm{e}^{\mathrm{u}\left(\mathrm{1}+\mathrm{u}\right)} \mathrm{du} \\ $$$${wait}……. \\ $$
Commented by 675480065 last updated on 02/Nov/20
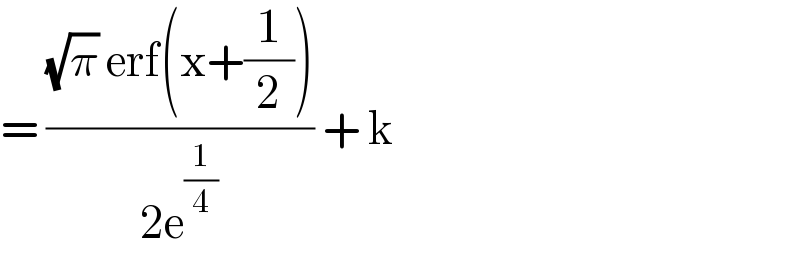
$$=\:\frac{\sqrt{\pi}\:\mathrm{erf}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2e}^{\frac{\mathrm{1}}{\mathrm{4}}} }\:+\:\mathrm{k} \\ $$
