Question Number 120920 by Khalmohmmad last updated on 04/Nov/20
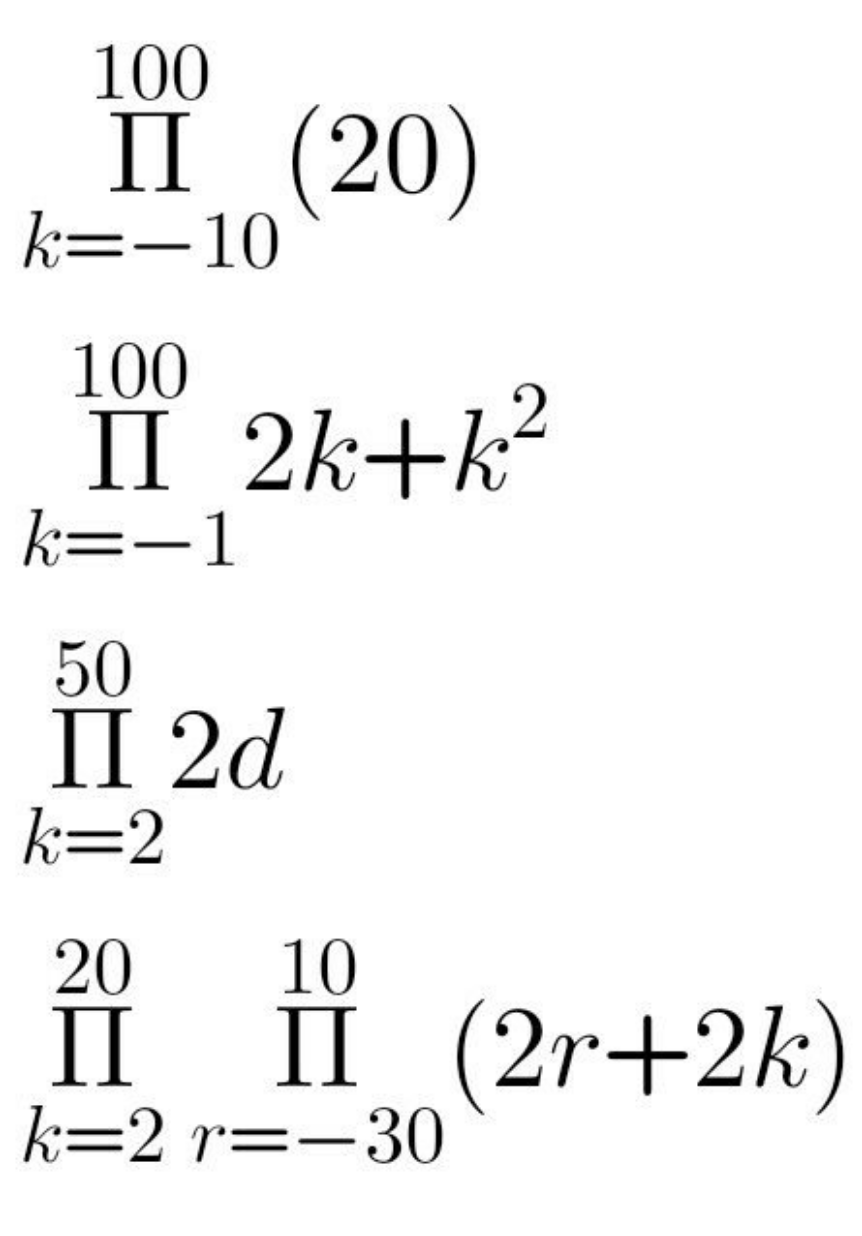
Answered by MJS_new last updated on 04/Nov/20

$$\mathrm{20}^{\mathrm{111}} \\ $$$$ \\ $$$$\mathrm{0}\:\mathrm{because}\:{k}=\mathrm{0}\:\Rightarrow\:{k}^{\mathrm{2}} +{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{we}'\mathrm{re}\:\mathrm{multiplying} \\ $$$$ \\ $$$$\mathrm{2}^{\mathrm{49}} {d}^{\mathrm{49}} =\mathrm{562949953421312}{d}^{\mathrm{49}} \\ $$$$ \\ $$$$\underset{{r}={a}} {\overset{{b}} {\prod}}\left(\mathrm{2}{r}+\mathrm{2}{k}\right)=\mathrm{2}^{{b}−{a}+\mathrm{1}} ×\frac{\left({k}+{a}\right)\left({k}+{b}\right)!}{\left({k}+{a}\right)!} \\ $$$$\mathrm{for}\:{a}<\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{some}\:{x}!\:\mathrm{with}\:{x}\in\mathbb{Z}^{−} \:\mathrm{and}\:\mathrm{both} \\ $$$$\mathrm{faculty}\:\mathrm{and}\:\Gamma\left({x}\right)\:\mathrm{are}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{Z}^{−} \\ $$
